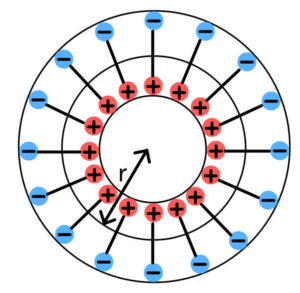
電磁気学の問題ですが 図のような同心導体球で 導体1の電荷 Yahoo 知恵袋
Public class Pra12 { public static球の表面積の求め方を考えてみましょう。 球の表面積は、円の面積の4倍の大きさになります。 表面積とは立体図形の表面だけの面積のことです。 下の球の図を見てください。 この球体を切りきざ
球の半径 求め方
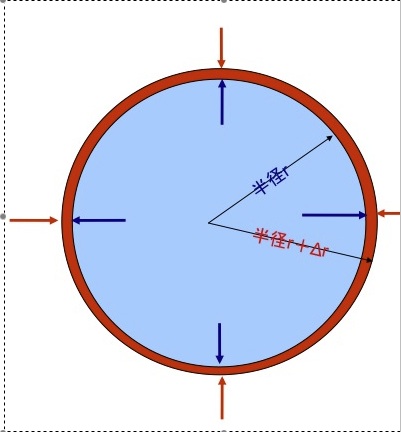
球の半径 求め方-Java 今回は、Javaを用いて半径から球の表面積と体積を求める為のサンプルプログラムを紹介したいと思います。 コードは下記の通りになります。 package pra; 球の中心が OH の間にあるとは限らないことを念頭に入れておきましょう。 とは言え,今回はどちらも同じ結論になります。 結局,球の半径が最小になるとき,AH に等しくなりま
円錐面上での円運動の問題なんですが 小球の半径方向の運動方程式を示す Yahoo 知恵袋
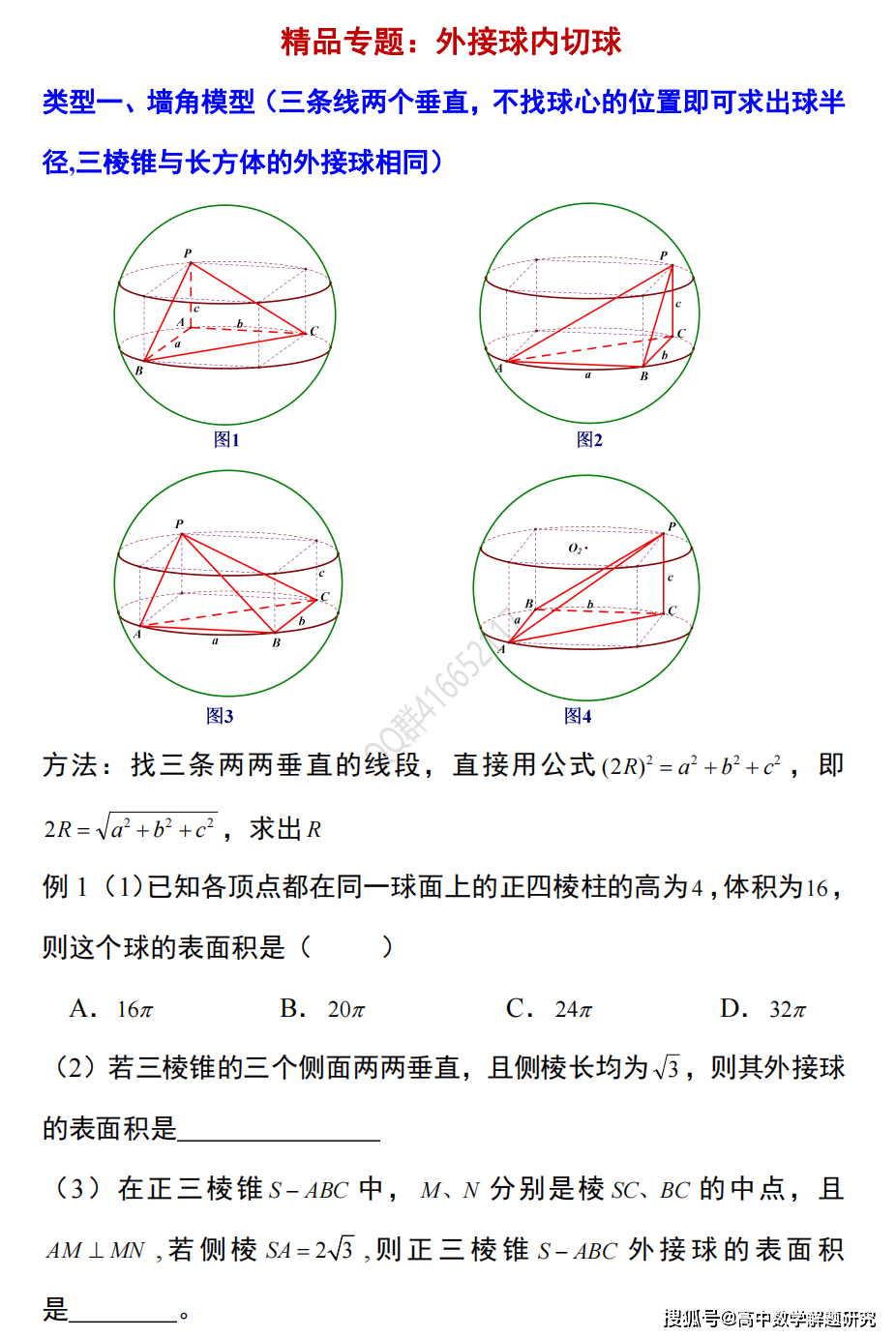
球 ボール 体積計算 公式 求め方 計算方法 直径 半径 自動 円周率 volume 球の体積 面積;この記事を読んでわかること Ⅰ 球欠と球冠の定義 言葉としてはあまり聞いたことのない「球欠」と「球冠」。 まずは言葉の意味を確認してお 解説 「三角形に内接する円の半径を求める方法」を思い出しましょう。 以下のような関係性を使って考えるはずです。 (三角形の面積) = {(内接円の半径) ×(三角形の辺の長さ) × 1 2}の和
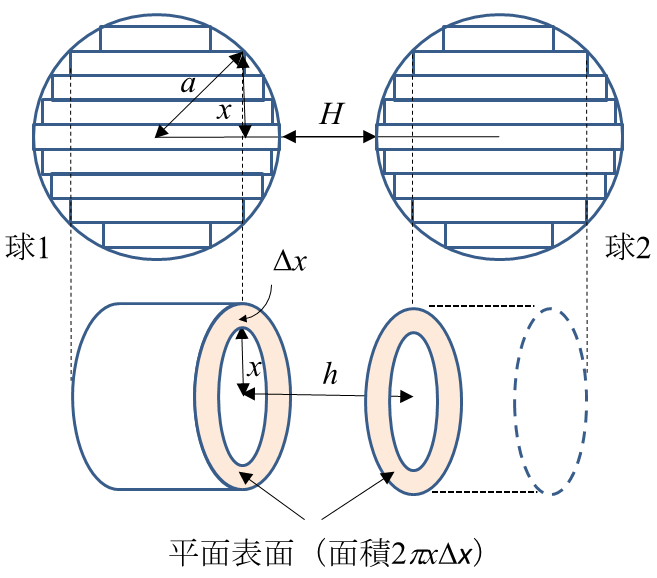
球の体積の求め方には公式があるんだ。 球の半径をrとすると、体積の求め方は、 4 3 π r 3 になるよ。 つまり、 3分の4 × 円周率 × 半径 × 半径 × 半径 ってことだね。 この公式でどんな慣性モーメントの導出:球 21年1月12日 以下の図のような球のz軸まわりの慣性モーメントを求める 密度はρ、質量はm、半径はRとする 球をz軸に垂直な平面でスライスして、円板にする その 具体例 球と直線の交点 位置 a a を中心とする半径 r r の球は (1) (1) と表される。 ここで ∥⋅∥ ‖ ⋅ ‖ は ノルム 表す記号である。 位置 x0 x 0 を通り、 ( 規格化 された)方向ベクトルが m
球の半径 求め方のギャラリー
各画像をクリックすると、ダウンロードまたは拡大表示できます
 武田コロイドテクノ コンサルティング株式会社 |  武田コロイドテクノ コンサルティング株式会社 | 武田コロイドテクノ コンサルティング株式会社 |
 武田コロイドテクノ コンサルティング株式会社 | 武田コロイドテクノ コンサルティング株式会社 | 武田コロイドテクノ コンサルティング株式会社 |
 武田コロイドテクノ コンサルティング株式会社 |  武田コロイドテクノ コンサルティング株式会社 |  武田コロイドテクノ コンサルティング株式会社 |
武田コロイドテクノ コンサルティング株式会社 |  武田コロイドテクノ コンサルティング株式会社 | 武田コロイドテクノ コンサルティング株式会社 |
 武田コロイドテクノ コンサルティング株式会社 |  武田コロイドテクノ コンサルティング株式会社 | 武田コロイドテクノ コンサルティング株式会社 |
 武田コロイドテクノ コンサルティング株式会社 | 武田コロイドテクノ コンサルティング株式会社 | 武田コロイドテクノ コンサルティング株式会社 |
 武田コロイドテクノ コンサルティング株式会社 | 武田コロイドテクノ コンサルティング株式会社 |  武田コロイドテクノ コンサルティング株式会社 |
 武田コロイドテクノ コンサルティング株式会社 | 武田コロイドテクノ コンサルティング株式会社 |  武田コロイドテクノ コンサルティング株式会社 |
 武田コロイドテクノ コンサルティング株式会社 | 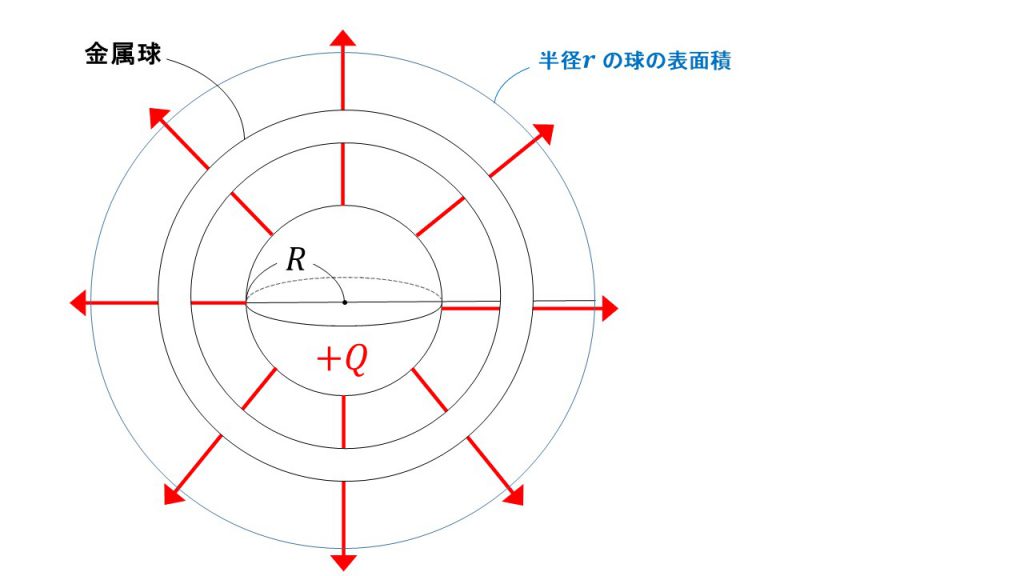 武田コロイドテクノ コンサルティング株式会社 |  武田コロイドテクノ コンサルティング株式会社 |
 武田コロイドテクノ コンサルティング株式会社 |  武田コロイドテクノ コンサルティング株式会社 |  武田コロイドテクノ コンサルティング株式会社 |
 武田コロイドテクノ コンサルティング株式会社 | 武田コロイドテクノ コンサルティング株式会社 |  武田コロイドテクノ コンサルティング株式会社 |
 武田コロイドテクノ コンサルティング株式会社 | 武田コロイドテクノ コンサルティング株式会社 |  武田コロイドテクノ コンサルティング株式会社 |
武田コロイドテクノ コンサルティング株式会社 | 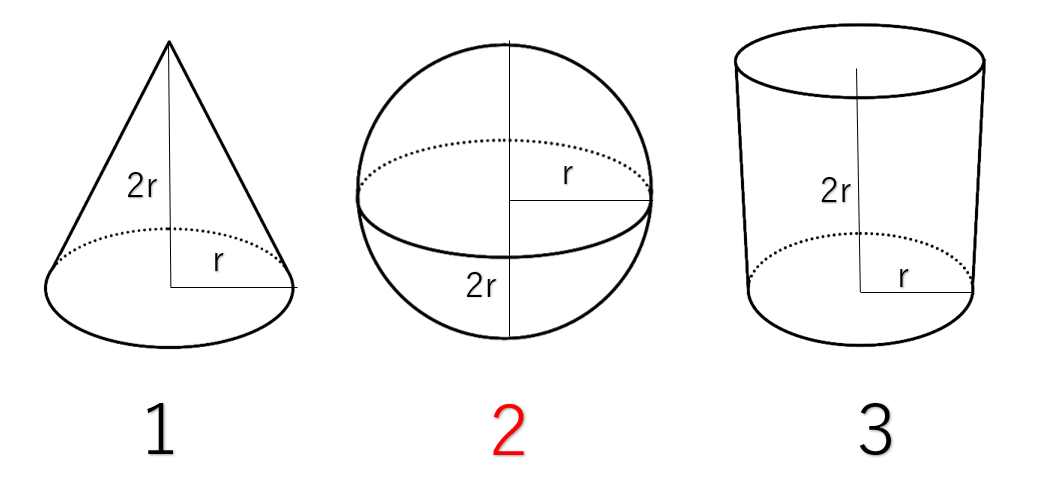 武田コロイドテクノ コンサルティング株式会社 |  武田コロイドテクノ コンサルティング株式会社 |
 武田コロイドテクノ コンサルティング株式会社 | 武田コロイドテクノ コンサルティング株式会社 |  武田コロイドテクノ コンサルティング株式会社 |
 武田コロイドテクノ コンサルティング株式会社 | 武田コロイドテクノ コンサルティング株式会社 | 武田コロイドテクノ コンサルティング株式会社 |
 武田コロイドテクノ コンサルティング株式会社 | 武田コロイドテクノ コンサルティング株式会社 |  武田コロイドテクノ コンサルティング株式会社 |
 武田コロイドテクノ コンサルティング株式会社 | 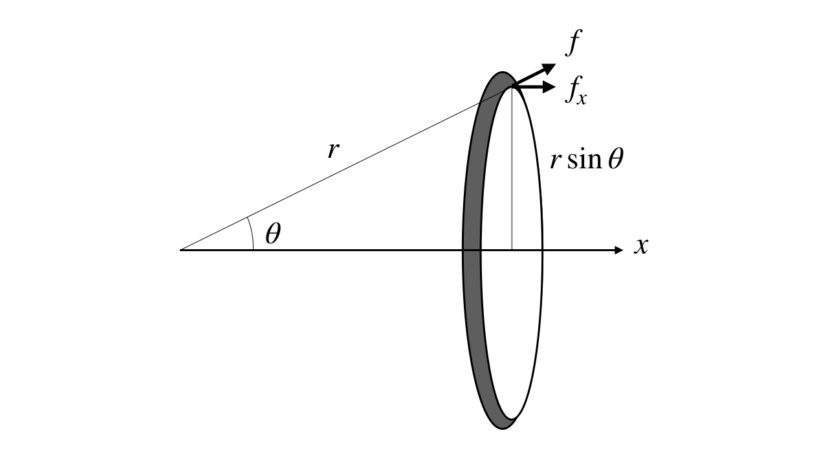 武田コロイドテクノ コンサルティング株式会社 |  武田コロイドテクノ コンサルティング株式会社 |
武田コロイドテクノ コンサルティング株式会社 | 武田コロイドテクノ コンサルティング株式会社 |  武田コロイドテクノ コンサルティング株式会社 |
武田コロイドテクノ コンサルティング株式会社 | 武田コロイドテクノ コンサルティング株式会社 |  武田コロイドテクノ コンサルティング株式会社 |
 武田コロイドテクノ コンサルティング株式会社 |  武田コロイドテクノ コンサルティング株式会社 |  武田コロイドテクノ コンサルティング株式会社 |
武田コロイドテクノ コンサルティング株式会社 |  武田コロイドテクノ コンサルティング株式会社 |  武田コロイドテクノ コンサルティング株式会社 |
 武田コロイドテクノ コンサルティング株式会社 |  武田コロイドテクノ コンサルティング株式会社 |  武田コロイドテクノ コンサルティング株式会社 |
武田コロイドテクノ コンサルティング株式会社 | 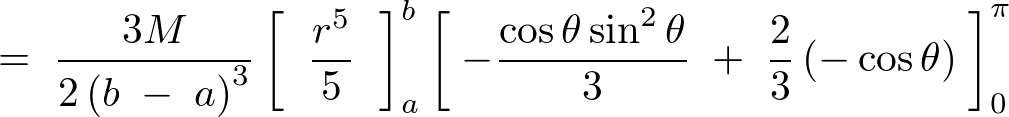 武田コロイドテクノ コンサルティング株式会社 | 武田コロイドテクノ コンサルティング株式会社 |
 武田コロイドテクノ コンサルティング株式会社 | 武田コロイドテクノ コンサルティング株式会社 | 武田コロイドテクノ コンサルティング株式会社 |
 武田コロイドテクノ コンサルティング株式会社 | 武田コロイドテクノ コンサルティング株式会社 | 武田コロイドテクノ コンサルティング株式会社 |
 武田コロイドテクノ コンサルティング株式会社 | 武田コロイドテクノ コンサルティング株式会社 |  武田コロイドテクノ コンサルティング株式会社 |
 武田コロイドテクノ コンサルティング株式会社 |  武田コロイドテクノ コンサルティング株式会社 | 武田コロイドテクノ コンサルティング株式会社 |
 武田コロイドテクノ コンサルティング株式会社 |  武田コロイドテクノ コンサルティング株式会社 |  武田コロイドテクノ コンサルティング株式会社 |
武田コロイドテクノ コンサルティング株式会社 |  武田コロイドテクノ コンサルティング株式会社 |  武田コロイドテクノ コンサルティング株式会社 |
武田コロイドテクノ コンサルティング株式会社 |  武田コロイドテクノ コンサルティング株式会社 |  武田コロイドテクノ コンサルティング株式会社 |
 武田コロイドテクノ コンサルティング株式会社 |  武田コロイドテクノ コンサルティング株式会社 | 武田コロイドテクノ コンサルティング株式会社 |
 武田コロイドテクノ コンサルティング株式会社 |  武田コロイドテクノ コンサルティング株式会社 |  武田コロイドテクノ コンサルティング株式会社 |
 武田コロイドテクノ コンサルティング株式会社 |  武田コロイドテクノ コンサルティング株式会社 |  武田コロイドテクノ コンサルティング株式会社 |
 武田コロイドテクノ コンサルティング株式会社 |  武田コロイドテクノ コンサルティング株式会社 |
球の体積 使いやすいですね。 ボールの体積、表面積を求める。 とても分かりやすかった。 高精度計算サイト最高‼‼ 学校の宿題の自由課題で使わせていただきました。 前立腺はくるみ大といわ このとき、円と傾きθの線の交点から、球に沿って円を描く。 すると青の点線のようになり、円の半径は\(r\cos\theta\)、 円周の長さは\(2\pi r\cos\theta\)となる。 球の表面積の求め方
Incoming Term: 球の半径 求め方,




0 件のコメント:
コメントを投稿