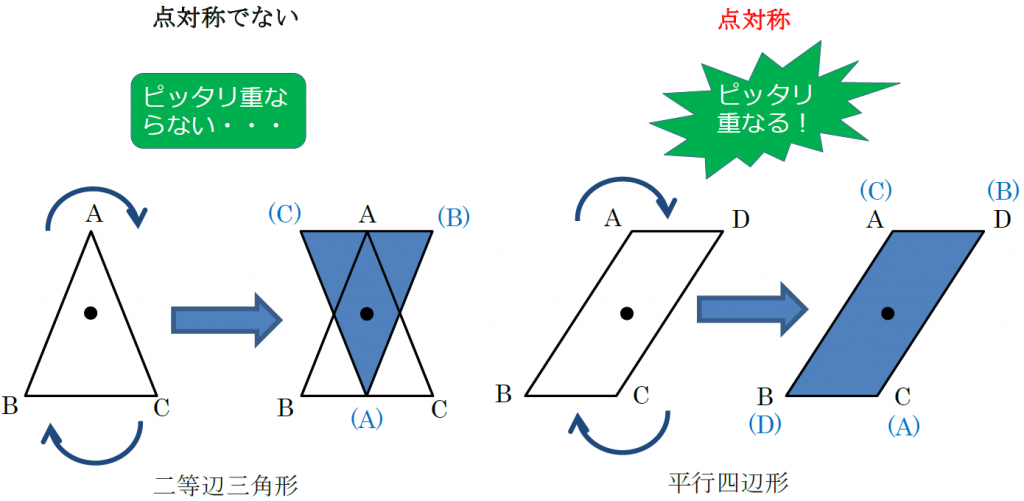
★点対称・線対称問題(11年 女子学院中学校) 親子で挑戦してみてください! 図1の正方形のまわりに,図2の正方形8個を図3の①~⑧の位置に置いて,大きい正方形の模様(もよう)を作ります。対称要素(symmetry element):幾何学的な意味での線(line), 面(plane),点(point)であって,これらの対称要素に関して1つ あるいはそれ以上の対称操作を行う.例えば回転(対称操 作)はある軸(対称要素)の回りに実行する. 426 4線対称・点対称の見分け方 図形の上に縦線を引く(イメージでOK) 図形を180°回転させる 線対称: 180°回転させるまでに左右対称になる瞬間がある(左右対称になった回数が対称の軸の本数) 点対称: 180°回転させた時、元の図形の形と一致する 左右
中1数学 点対称な図形とは まなビタミン
中学生 点対称 問題
中学生 点対称 問題-小学6年生 算数<8月>線対称/点対称円の面積 練習問題プリント 線対称/点対称の文章題、作図、円の面積、文章題1(a) 対称錐計画問題とは Faybusovich(1997) "Linear systems in Jordan algebras and primaldual interiorpoint algorithms" 特徴 B 目的関数は線形 B 条件は線形制約と対称錐制約 (非負制約,2次錐制約,半正定値制約など) B 線形計画・2次錐計画・半正定値計画を含む B 主双対内点法により,多項式時間で最適解が求まる



中1数学 点対称な図形とは まなビタミン
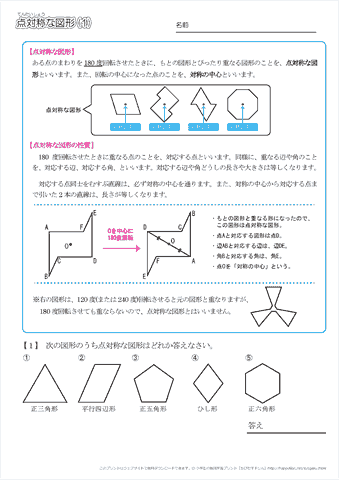
小6 算数「線対称・点対称」2 組 番氏名 (1)点o を対称の中心とした点対称な図形の残りの半分をかきましょう。 (2)次の正多角形について,線対称や点対称のときは ,そうでないときは×をかきま しょう。また,線対称のときは,対称の軸の数をかき問!3点対称な図形はどれですか。 すべて答えましょう。!2線対称な図形はどれですか。 すべて答えましょう。!4線対称でもあり,点対称でもある図形はどれですか。 算数 第6学年 対称な形 月 日 名前 問 下の3つの正多角形について,質問に答えなさい。第2講 点対称のテスト対策・練習問題ならスタディサプリ。 問題を解くコツ、公式、暗記法などをまとめて解説。 わかりやすい映像授業とテキスト(プリント・冊子)で書き込みながら学びます。
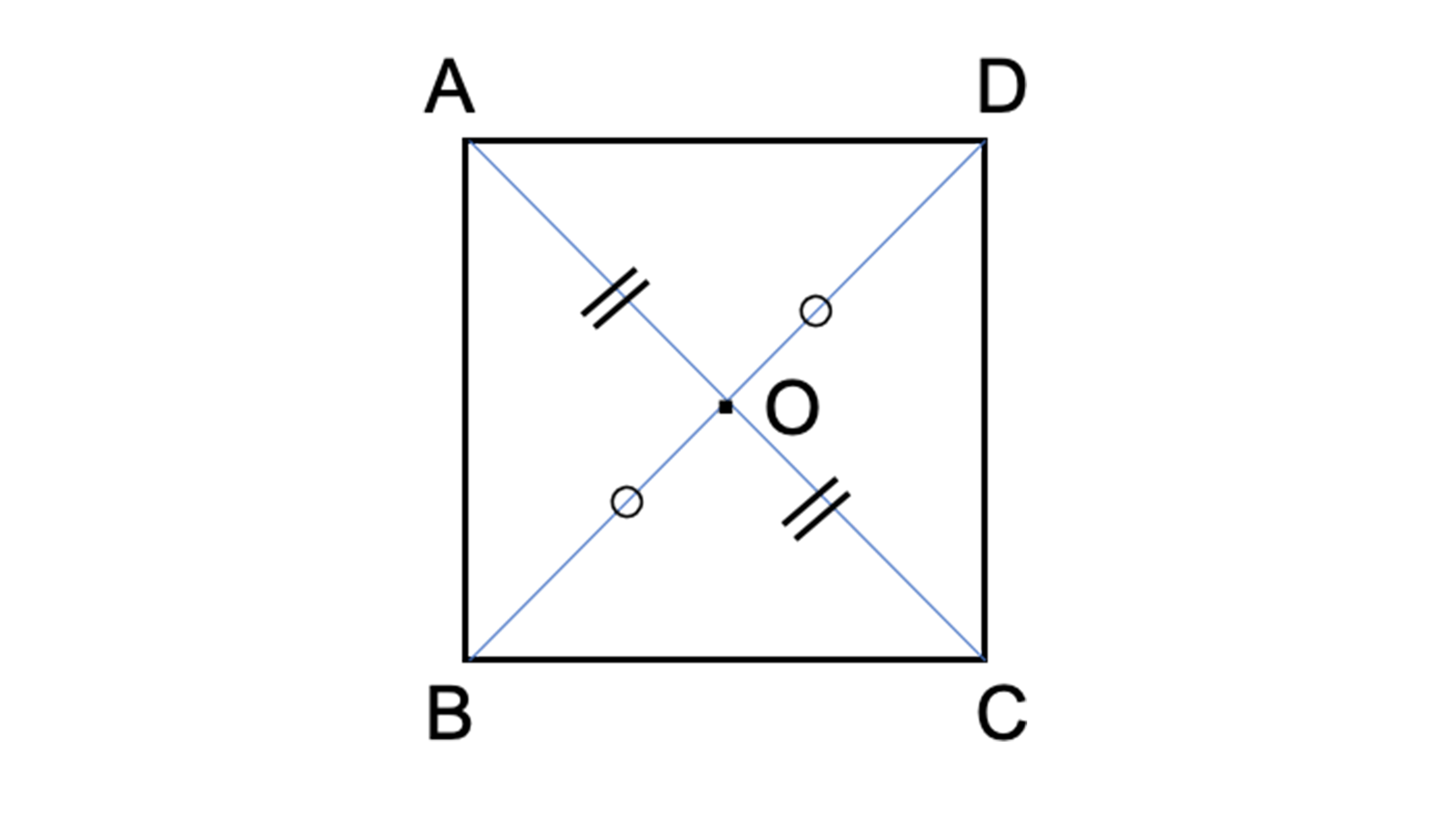
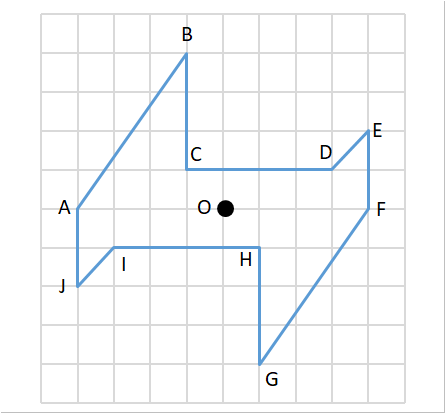
評価問題 下の図は、点対称な図形です。 ①辺BCと対応している辺はどこですか。また長さは何㎝ですか。 ②角Dと対応している角はどこですか。また、何度ですか。 ③対称の中心Oを見つけましょう。 ④点Gと対応する点Hを見つけましょう。小学6年生で習う、点対称な図形のかき方を練習できるプリントです。 作図が苦手なお子さんでも、色々な形の点対称な図形を練習することで、苦手意識をなくします。 「かんたん」「ふつう」「むずかしい」でプリントが分かれているため、学習進度によって選べます。 関連学習プリント 「点対称な図形の作図の練習問題」の講座と合わせて学習したいオススメ点対称な図形と対称の中心の意味について理解する。 小学生・中学生が勉強するならスクールTV。 全国の学校の教科書に対応した動画で学習できます。
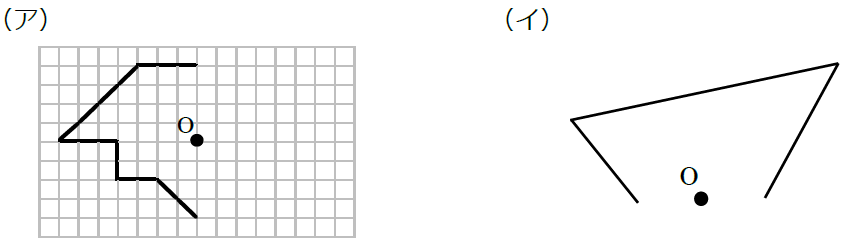
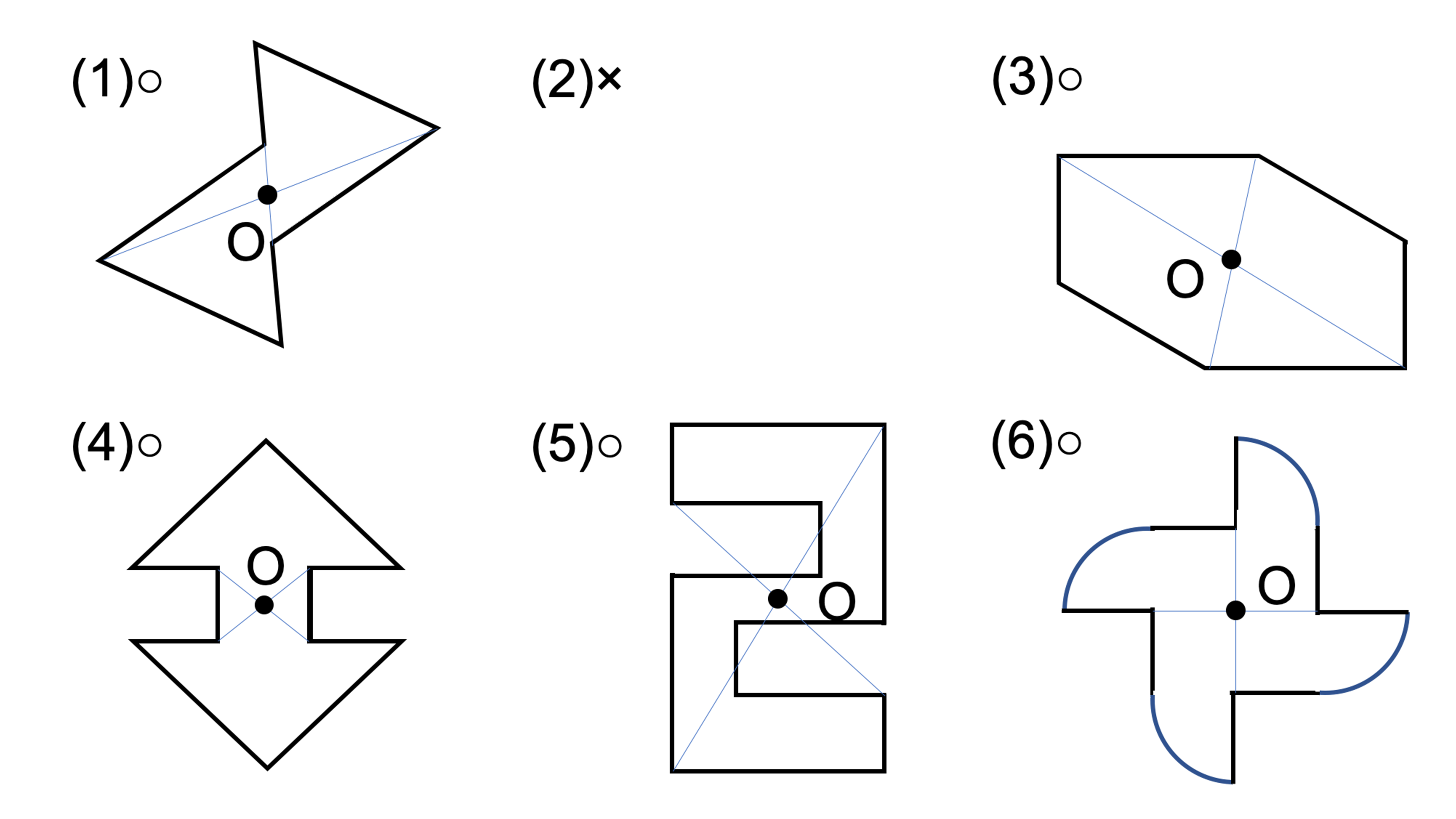
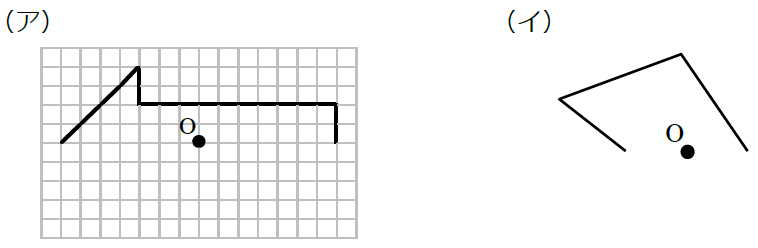
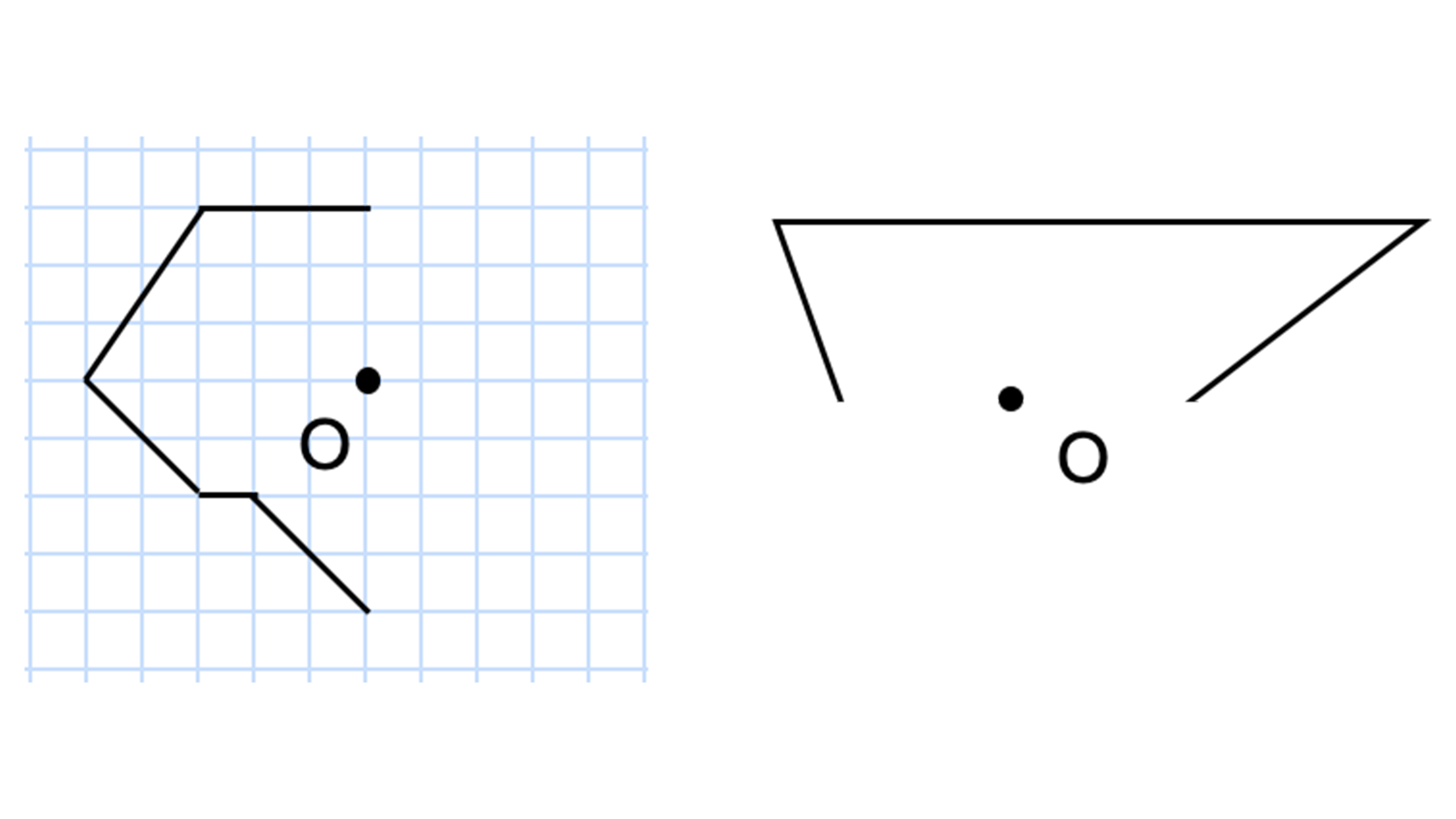
対称点の軌跡の問題で・・・ 0037 問題文 直線y=χ1 に関して,点Pと対称な点Qをとる。 点Pが直線y=2χ 上を動くとき,点Qの軌跡を求めよ。 頑張ってみましたが、解けませんでした点対称な図形 ※右の図形は、1度(または240度)回転させると元の図形と重なりますが、 180度回転させても重ならないので、点対称な図形とはいいません。 1次の図形のうち点対称な図形はどれか答えなさい。 答え 点対称な図形 対称の中心 対称の中心 対称の中心 対称の中心 a b c d e f o a b d c e f o oを中心にそこで、問題が100を超えた所で、点対称でない問題も作っていこうと思います。 作成問題の変更 2) 問題が0を超えたので、別の方式の問題を考えました。 四角の形を変えることを考えてみましたが、これは色々と問題がありそうです。



中学生の数学講座 線対称 点対称



線対称図形と点対称図形の見分け方 算数解法の極意
回転対称ある格子点を中心に回して重なる。 (ただし、360度回転は含まない) n回回転操作を繰り返して元に戻るとき、 "n回回転対称軸"と呼ぶ。 n=2,3,4,6 鏡映対称格子点の配置が格子のある面に対して 左右対称である(停留点の導出) 最小化問題 , = 3−3 3 目的関数の勾配ベクトルは , = 3 2−3 3 2−3 , =0を解くと , =0,0,(1,1) 問題は、「停留点であっても局所最適解とは限らない」こと。 10 図3:f(x,y)のグラフ3 点対称な図 形 ( 教p14~16) 7 ・点対称な図形の対応する点,辺, 角を調べる。 関 点対称な図形において,対応する点, 辺,角を見つけようとしている。 知 点対称な図形において,対応する点, 辺,角の意味や性質について理解し ている。 8



小6算数 対称な図形 点対象 指導アイデア みんなの教育技術



Www Pref Saitama Lg Jp Documents R2suugaku7b Pdf
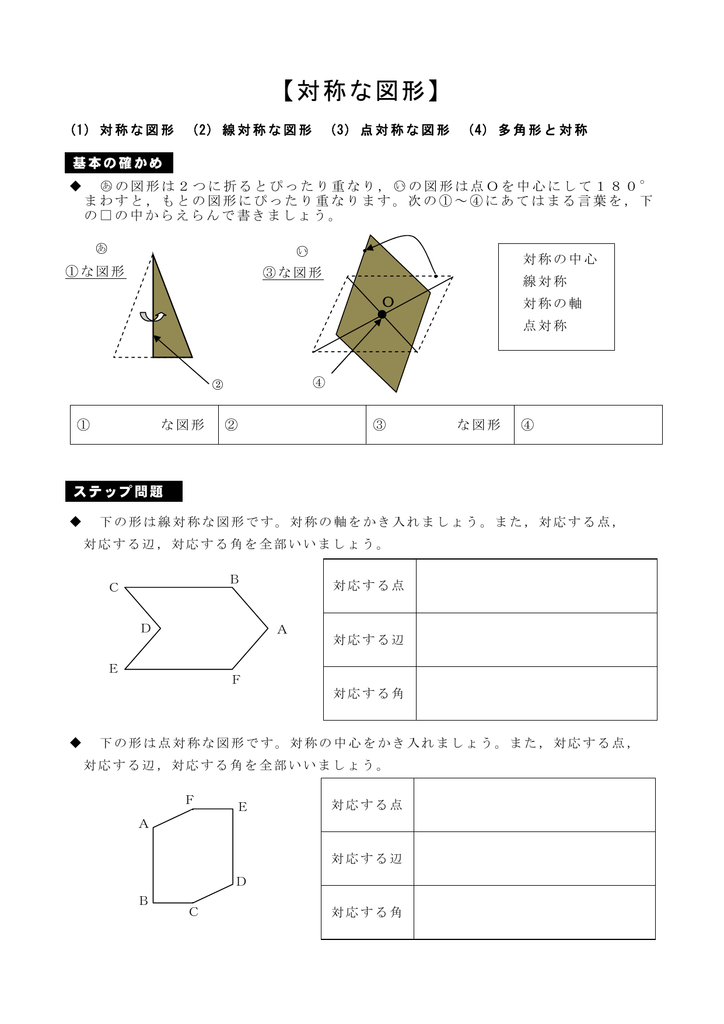
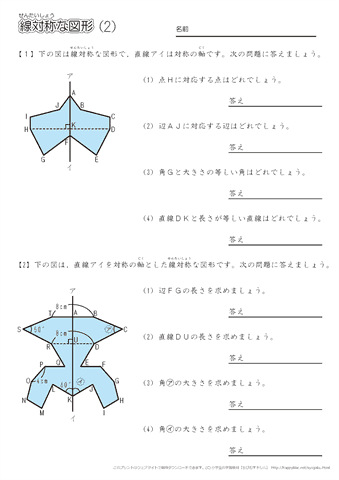
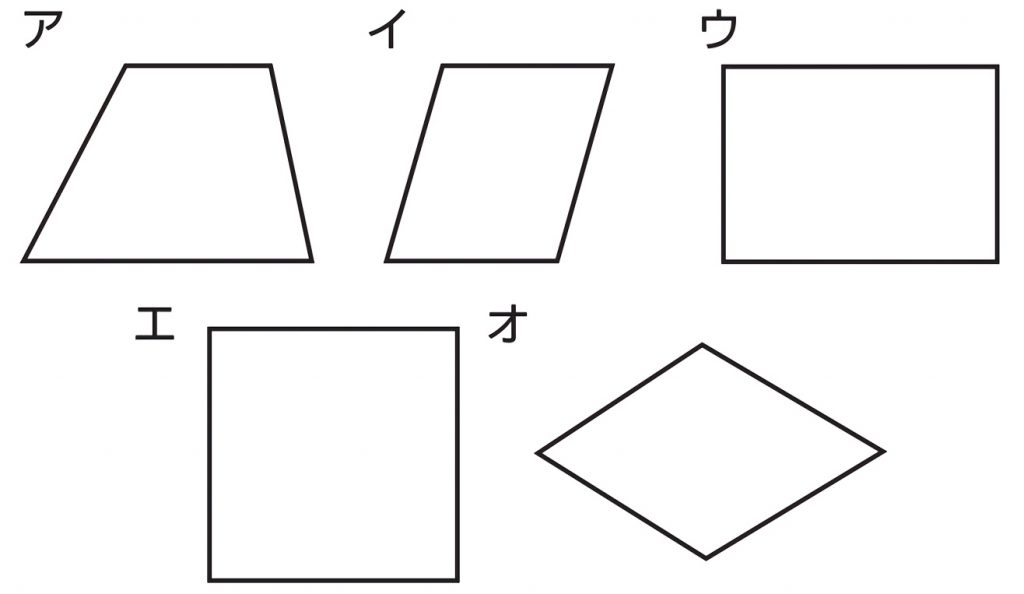
11問 6年「対称な図形」 氏名 1 次の図形から,点対称な図形と線対称な図形を答えましょう。 線対称な図形 点対称な図形 2 下の図は線対称な図形です。 ⑴ 対称の軸は,どれですか。 ⑵ 点Fに対応する点は,どれですか。対称性(どのような対称要素を持つか)による分類=点群 C1:対称性を持たない(恒等Eはある) 回転軸(C2以上)を待たない Cs:対称面σをもつ Ci:対称心iをもつ Cn:n回回転軸 Cnv:主軸 Cnとn枚のσv Cnh:主軸 Cnと1枚のσh 回転軸を待つ (プリント) Cl Cs CiAmazonで認知工学の8/31まで おためし問題集特典つき天才ドリル 平面図形が得意になる点描写 線対称 小学校全学年用 算数 (考える力を育てる)。アマゾンならポイント還元本が多数。認知工学作品ほか、お急ぎ便対象商品は当日お届けも可能。また8/31まで おためし問題集特典つき




Primary算数的小六の復習 線対称 点対称な図形 筆記 Clear



1
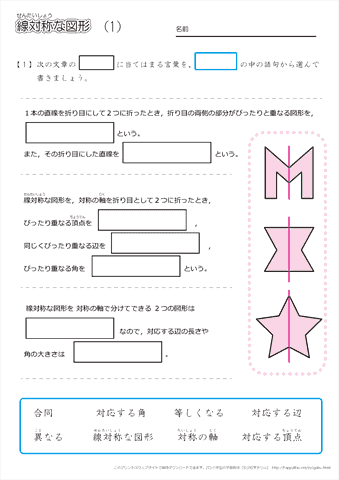
1 対称な図形 学 年 組 氏 名 1 次の文字について,線対称な形には ,点対称な形には ,どちらでもないときは× を答えましょう。 線対称な形とは,1本の直線を折り目にして二つ折りにしたとき,両側の部分がぴったりと重なる形です。点対称な形 点対称 対象性と角度の関係をつかむ! (筑波大学附属中学 14年) 下の図のように、角アと点A があります。 直線OXについて点B と対称な点をEとします。 直線OYについて点C と対称な点をF とします。 3点E,O,F が一直線上にあるとき、角アの大きさを点対称な図形 ※右の図形は、1度(または240度)回転させると元の図形と重なりますが、 180度回転させても重ならないので、点対称な図形とはいいません。 1次の図形のうち点対称な図形はどれか答えなさい。 答え 点対称な図形



対称な図形



無料 中1数学 標準問題 解答プリント 135 平面図形2 多角形 点対称
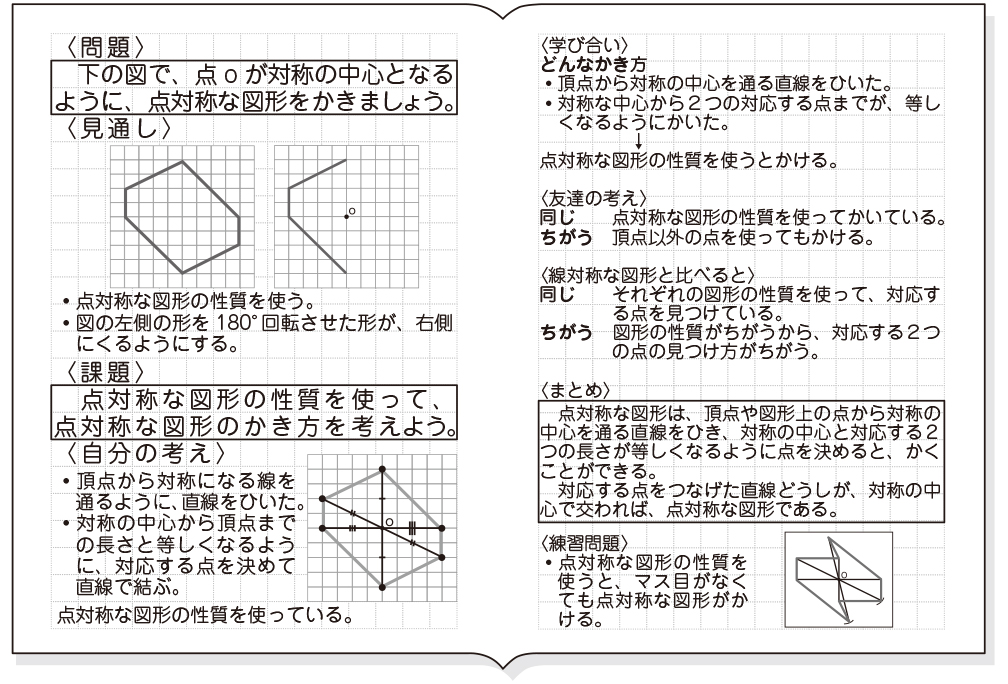
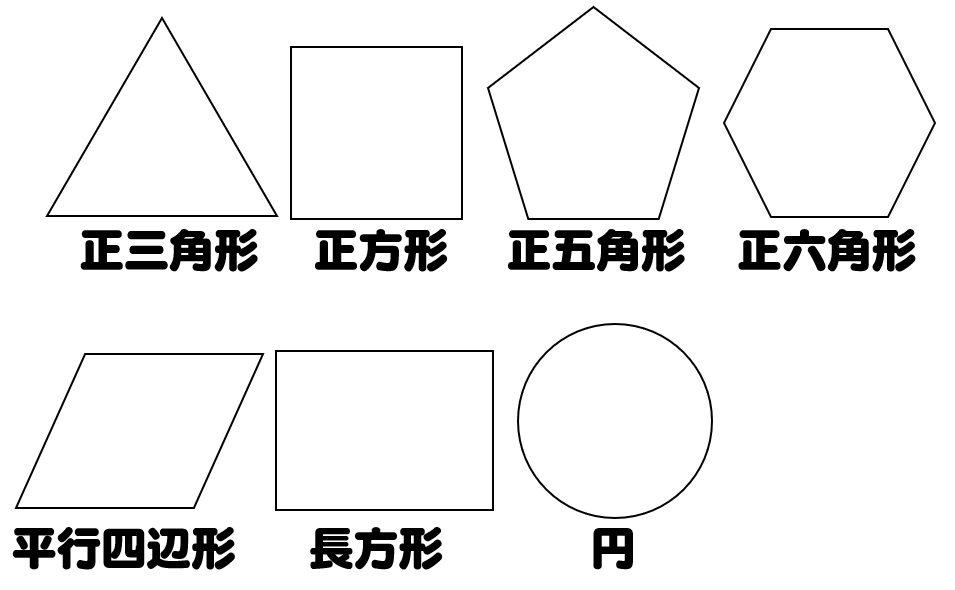
点Oが対称の中心になるように,点対称な図形をかきましょう。 次の図形について,下の表を完成させましょう。 正三角形 正方形 平行四辺形 ひし形 線対称かどうか 対称の軸の本数(本) 2 点対称かどうか ア イ ・ O ステップ問題



線対称 点対称 昇英塾
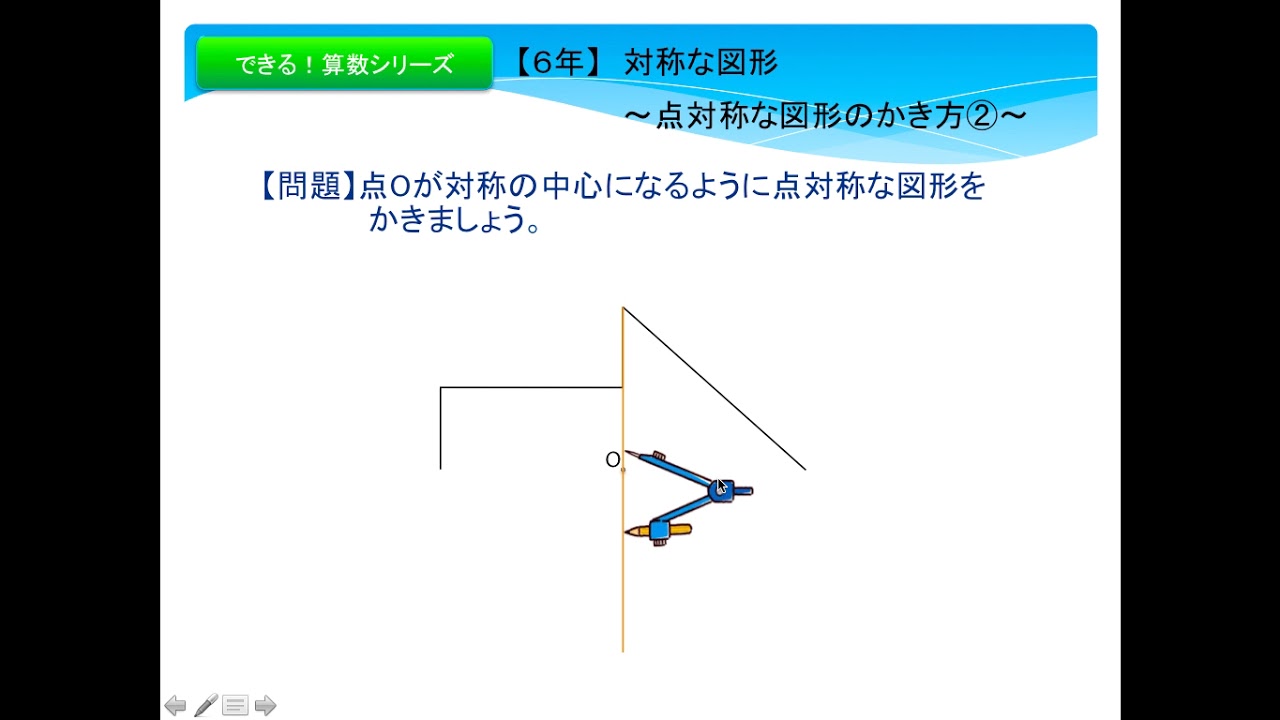



スマホok 6年 対称な図形 点対称な図形のかき方 Youtube



線対称との違いは 点対称 な図形を理解しよう お役立ち情報ページ 個別指導の学習塾なら個別指導塾スタンダード



線対称との違いは 点対称 な図形を理解しよう お役立ち情報ページ 個別指導の学習塾なら個別指導塾スタンダード



小学6年生の算数 点対称な図形 問題プリント ちびむすドリル 小学生



ドリルズ 小学6年生 算数 の無料学習プリント対称な図形 点対称



無料 中1数学 基本問題 問題プリント 平面図形2 多角形 点対称 135



点対称な図形のかき方 Youtube




中1数学 点対称な図形とは まなビタミン
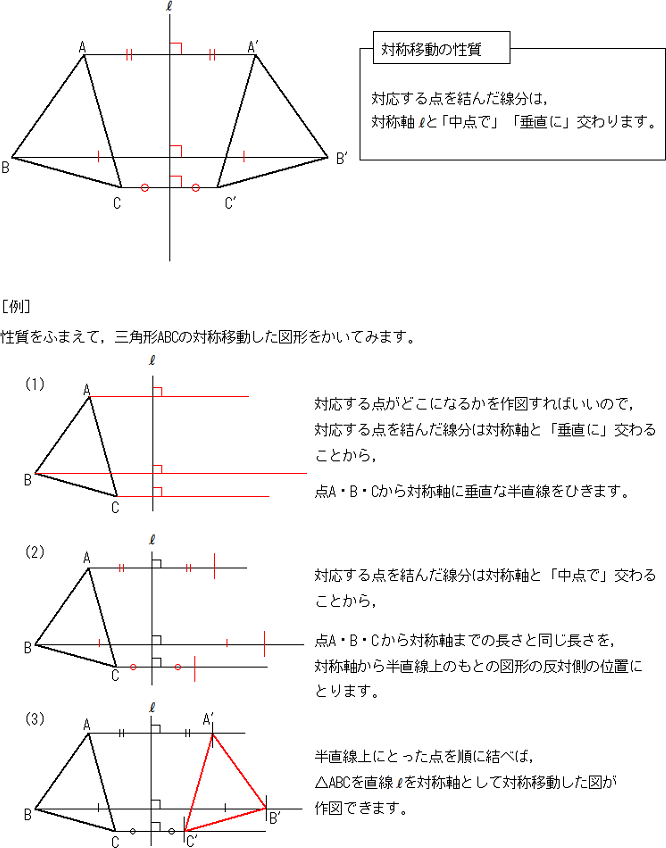



平面図形 対称移動とは何ですか 中学数学 定期テスト対策サイト
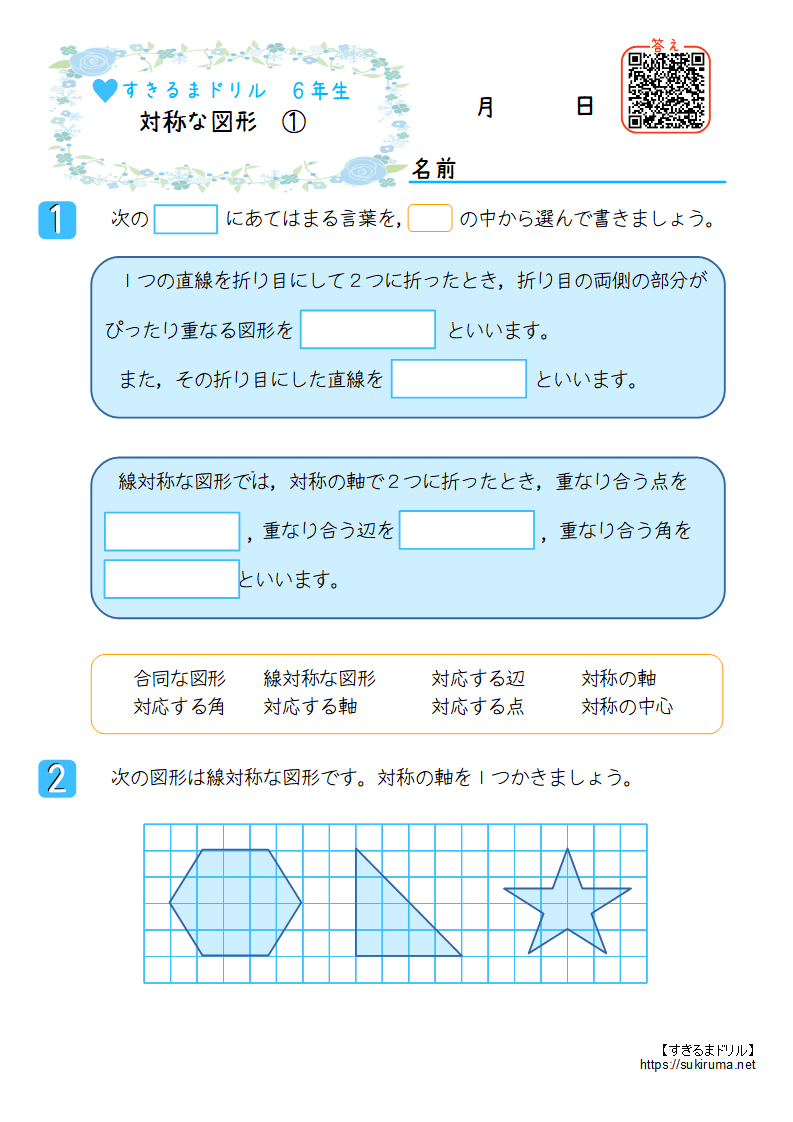



すきるまドリル 小学6年生 算数 対称な図形 無料学習プリント すきるまドリル 無料学習プリント
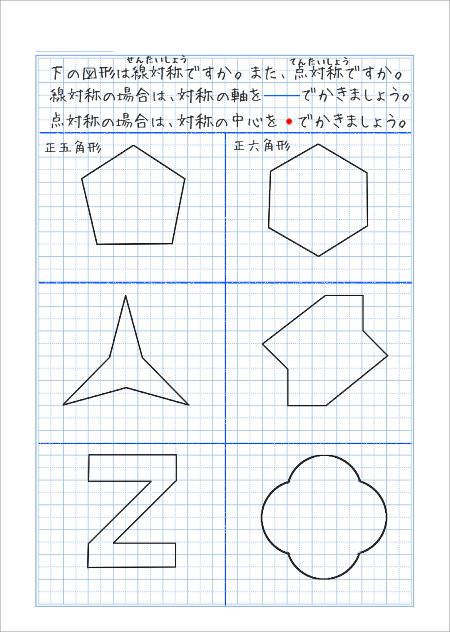



線対称と点対称の自主学習ノート 家庭学習レシピ



対称な図形 たしかめよう 6年生 翁島 おきなしま 小学校ホームページ




世界一分かりやすい算数 小6 対称な図形
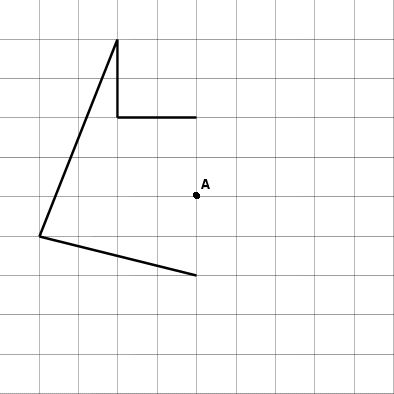



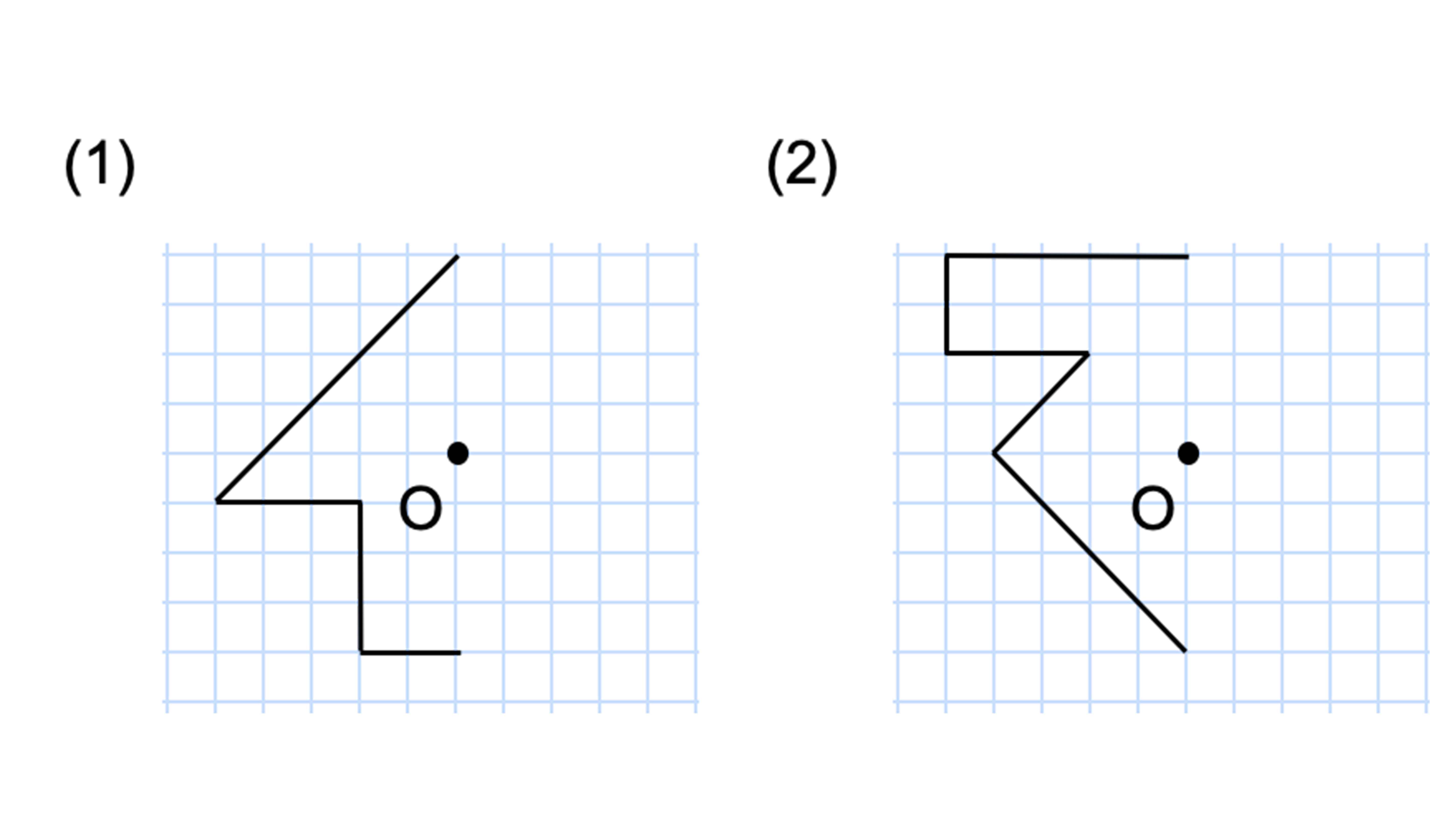
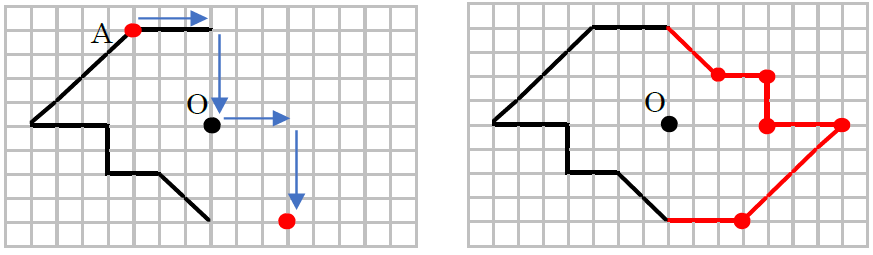
点対称な図形を書く
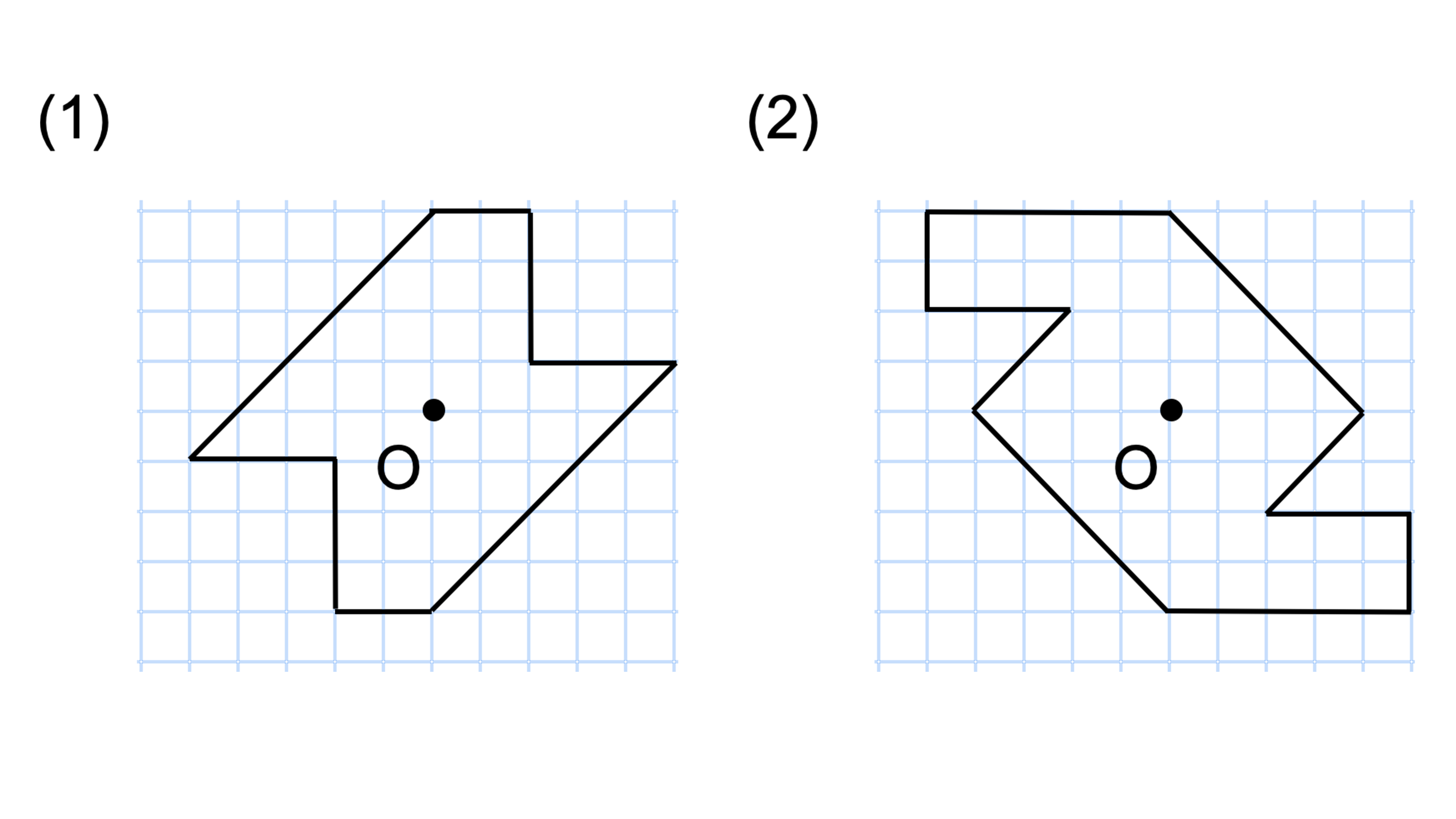



線対称との違いは 点対称 な図形を理解しよう お役立ち情報ページ 個別指導の学習塾なら個別指導塾スタンダード




対称な図形 線対称と点対称 小学生 算数のノート Clear




点対称の図形の書き方を教えてください Clear
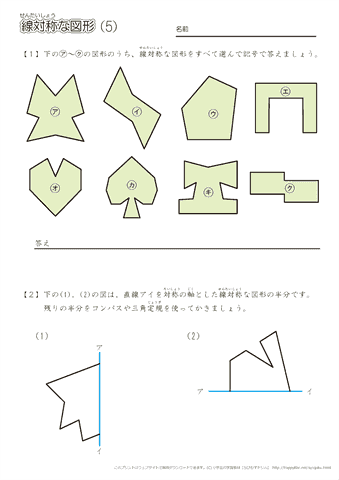



小学6年生の算数 線対称な図形 問題プリント ちびむすドリル 小学生



小学6年生の算数 線対称な図形 問題プリント ちびむすドリル 小学生




中1数学 点対称な図形とは まなビタミン



点対称な図形



点対称 算数解法の極意
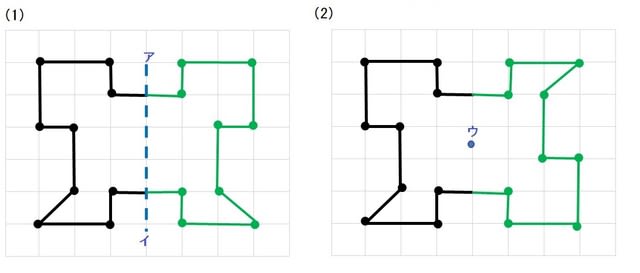



何かと教えづらい 線対称 点対称 小6 算数の教え方教えますmother S Math Happy Study Support



対称な図形と授業運営 教育考現学
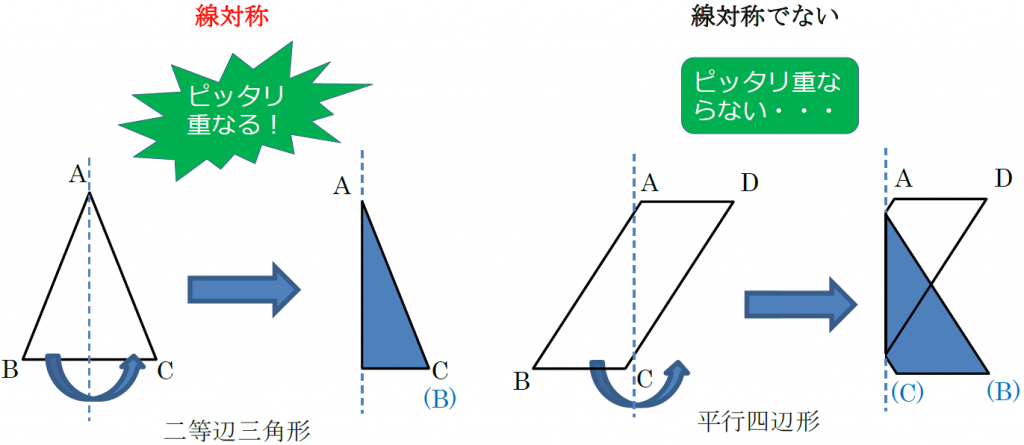



中1数学 点対称な図形とは まなビタミン
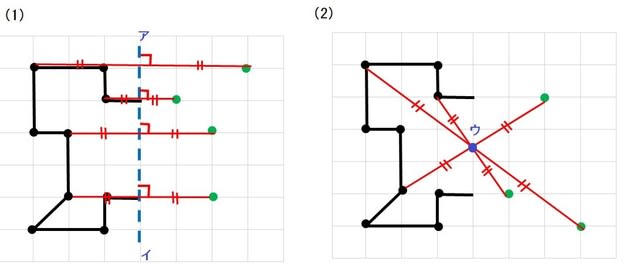



何かと教えづらい 線対称 点対称 小6 算数の教え方教えますmother S Math Happy Study Support



1



ドリルズ 小学6年生 算数 の無料学習プリント対称な図形



多角形と対称 6年生 翁島 おきなしま 小学校ホームページ



Http Www Kita9 Ed Jp Eductr Handbook Challengesheet Elementaryschool Sansuu 6 601 Pdf
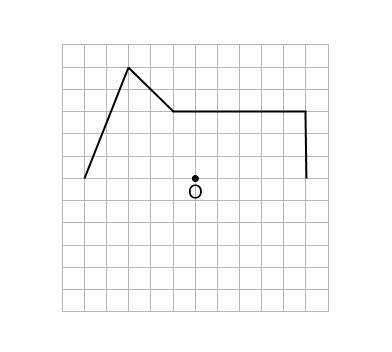



中学数学 点対称な図形 中学数学の無料オンライン学習サイトchu Su




世界一分かりやすい算数 小6 対称な図形



点対称な図形のかき方 Youtube




線対称 点対称とは 具体例6選と応用問題3選で解説します 遊ぶ数学



無料 中1数学 基本問題 解答プリント 平面図形2 多角形 点対称 135



天才ドリル 平面図形が得意になる点描写 線対称 小学校全学年用 算数 絵本ナビ 認知工学 みんなの声 通販



点対称な図形の対応する頂点を確認する Ipadとiphoneで教師の仕事をつくる



Www Tsukuba Ed Jp Kuki2 Wp Content Uploads 04 Ba397da52e47dce9954f2b80fe45da14 Pdf
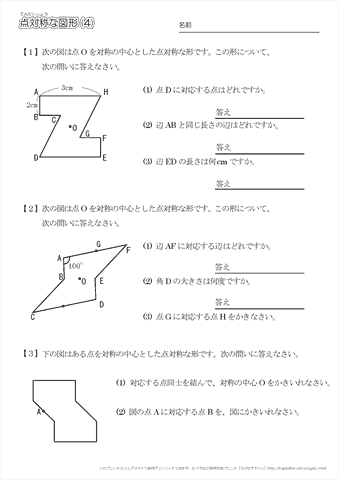



小学6年生の算数 点対称な図形 問題プリント ちびむすドリル 小学生




線対称で点対称な図形をかく 算数を究める



対称図形のドリル
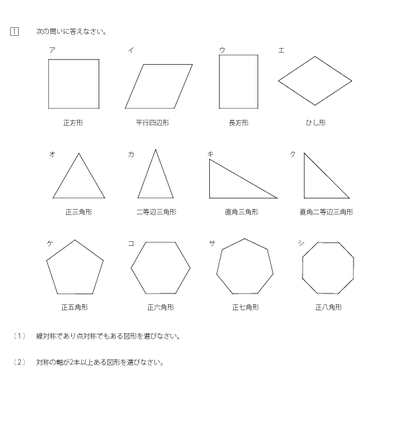



みんなの算数オンライン 教科書 多角形の線対称 点対称




世界一分かりやすい算数 小6 対称な図形




世界一分かりやすい算数 小6 対称な図形



小学6年生の算数 線対称な図形 問題プリント ちびむすドリル 小学生



線対称との違いは 点対称 な図形を理解しよう お役立ち情報ページ 個別指導の学習塾なら個別指導塾スタンダード




世界一分かりやすい算数 小6 対称な図形




対称な図形 線対称と点対称 小学生 算数のノート Clear



線対称との違いは 点対称 な図形を理解しよう お役立ち情報ページ 個別指導の学習塾なら個別指導塾スタンダード




対称の中心を使わずに点対称な図形をかく 算数を究める



対称図形のドリル



中1数学 平面図形3 点対称 点対称2 発展問題 問題 137 プリント



中1数学 点対称な図形とは まなビタミン



Math 点対称な図形のかき方 働きアリ



中1数学 平面図形3 線対称 点対称 発展問題 問題 136 プリント




8 31まで おためし問題集特典つき 天才ドリル 平面図形が得意になる点描写 線対称 小学校全学年用 算数 考える力を育てる 認知工学 本 通販 Amazon



Fdk3a7ctb5192box5b Com Es 6nen Mt Tentaishou Sakuzu Html



3



中1数学 点対称な図形とは まなビタミン
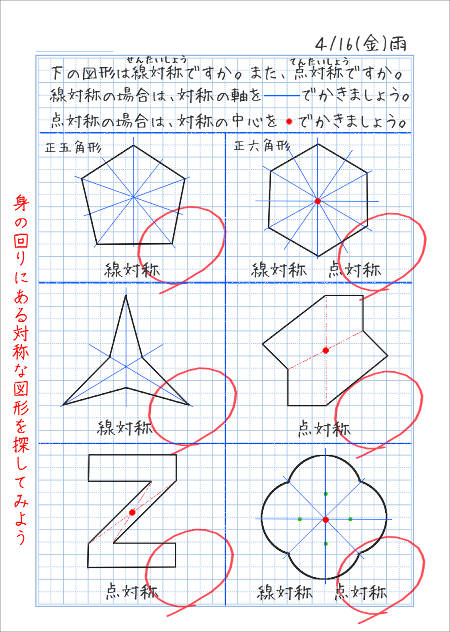



線対称と点対称の自主学習ノート 家庭学習レシピ



Math 点対称な図形のかき方 働きアリ




世界一分かりやすい算数 小6 対称な図形
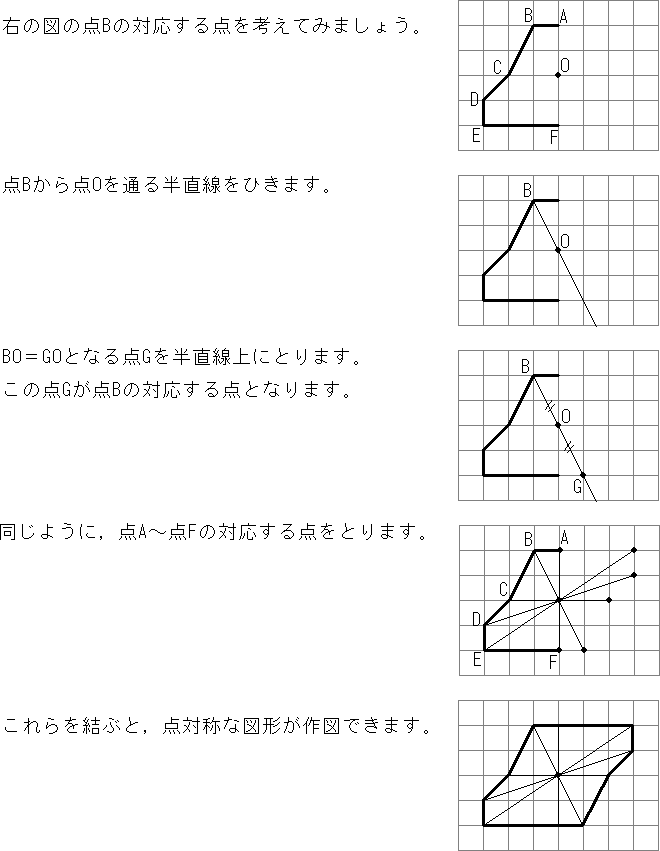



点対称な図形のかき方 中学数学 定期テスト対策 ベネッセ教育情報サイト
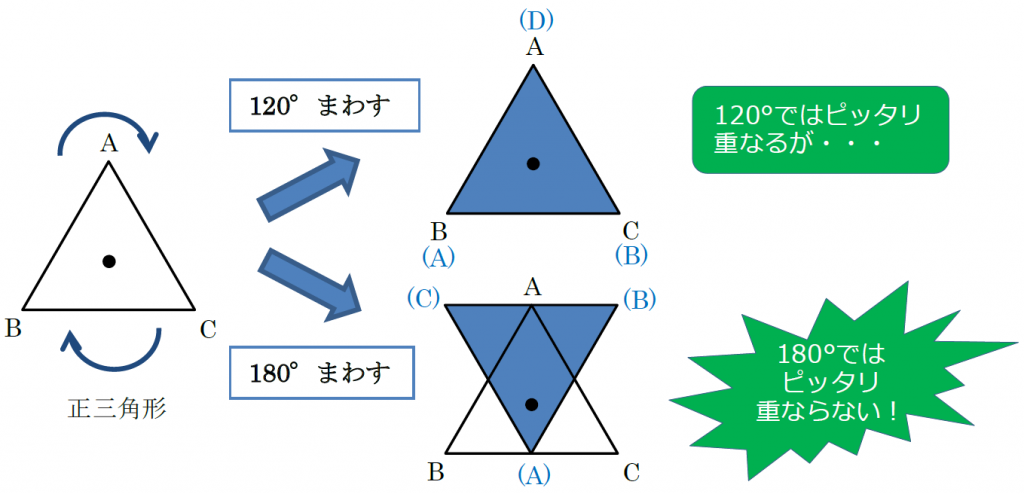



中1数学 点対称な図形とは まなビタミン



Fdk3a7ctb5192box5b Com Es 6nen Mt Tentaishou Sakuzu Html
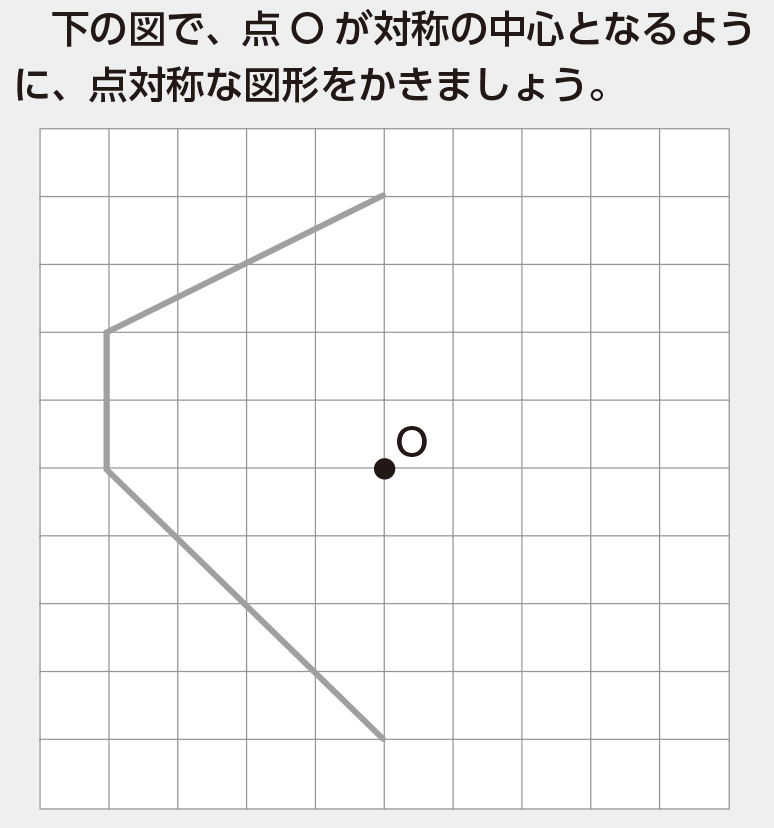



小6算数 対称な図形 点対象 指導アイデア みんなの教育技術



無料 中1数学 基本解説 問題プリント 平面図形2 多角形 点対称 135
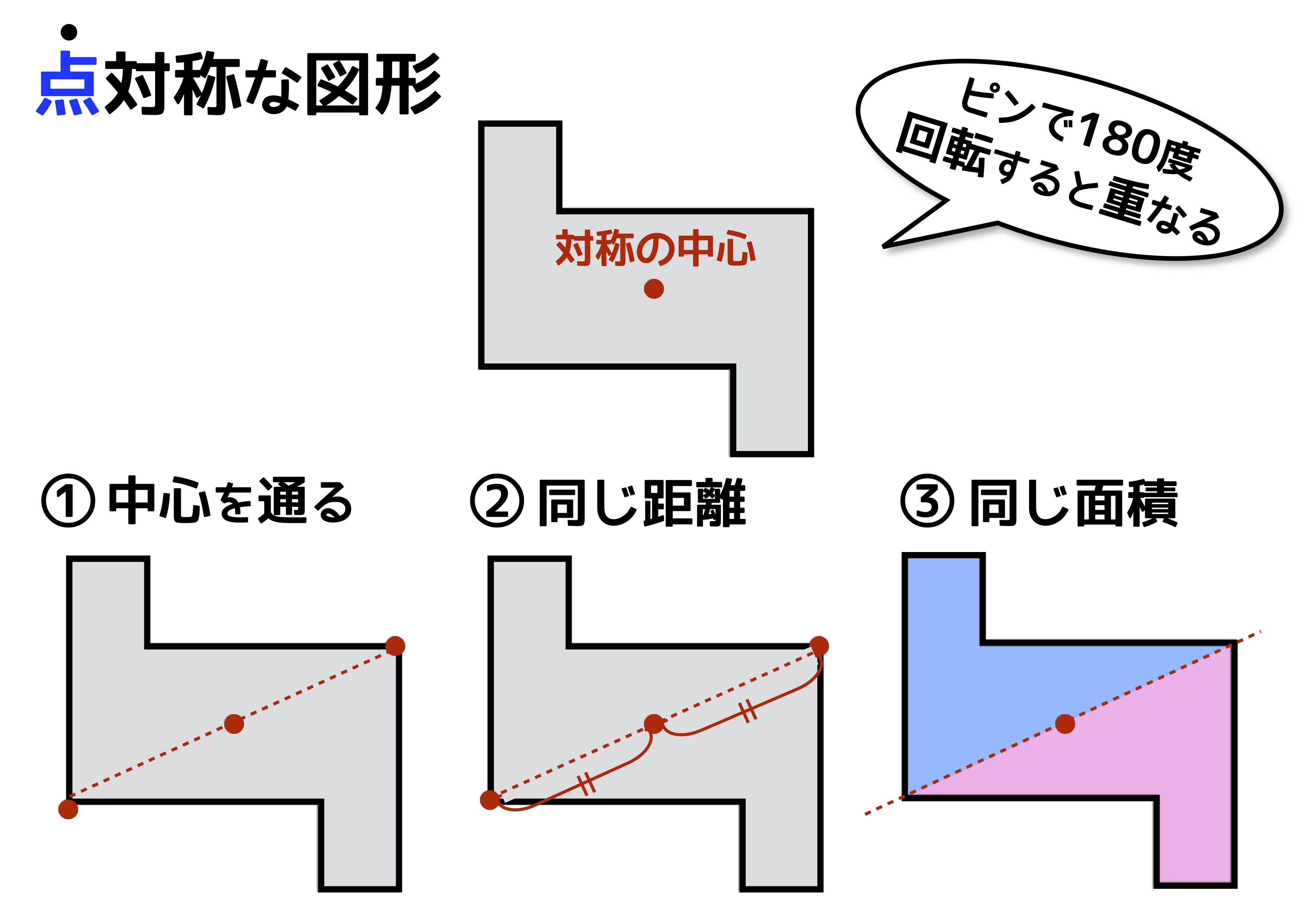



線対称と点対称 3つの性質を上手に使えるかどうかで得点に大きな差が出る 中学受験ナビ



中山先習塾 練習問題 テストが作動しないときは Internet Explorerをお試しくださいワン 小6 B 対称な図形 点対称 対称の軸 対応する点 中心を通り同距離 100 点満点 合格点 設定なし 残り時間 テスト開始 テストを開始するには



線対称との違いは 点対称 な図形を理解しよう お役立ち情報ページ 個別指導の学習塾なら個別指導塾スタンダード




スマホok 6年 対称な図形 算数をつかってやってみよう 線対称や点対称な図形をかいてみよう Youtube



線対称 点対称の定義と違い 簡単な見分け方を解説 数学fun



小6算数 多角形と対称 指導アイデア みんなの教育技術



アルファベットのa H R Zの中で 点対称な図形と線対称な図形 線対 Yahoo 知恵袋



Fdk3a7ctb5192box5b Com Es 6nen Mt Tentaishou Sakuzu Html




問題の解き方を教えてください Clear




8 31まで おためし問題集特典つき 天才ドリル 平面図形が得意になる点描写 点対称 小学校全学年用 算数 考える力を育てる 認知工学 本 通販 Amazon




スマホok 6年 対称な図形 多角形と対称 Youtube




対称な図形 Ict教材eboard イーボード
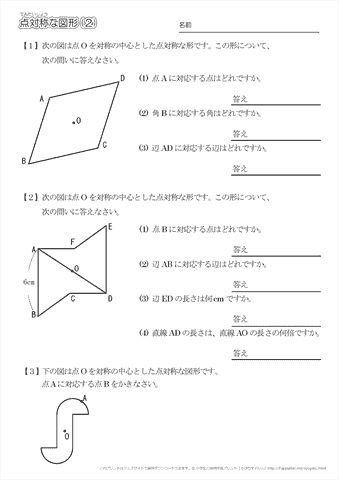



小学6年生の算数 点対称な図形 問題プリント ちびむすドリル 小学生



無料 中1数学 発展問題 問題プリント 平面図形4 円 対称
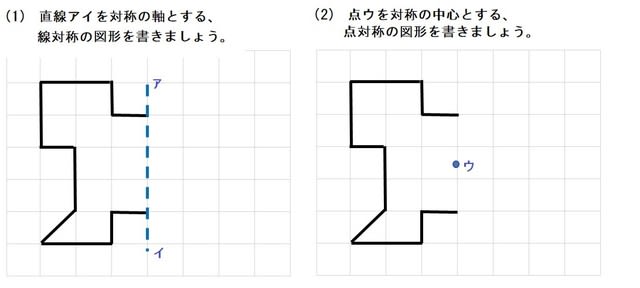



何かと教えづらい 線対称 点対称 小6 算数の教え方教えますmother S Math Happy Study Support
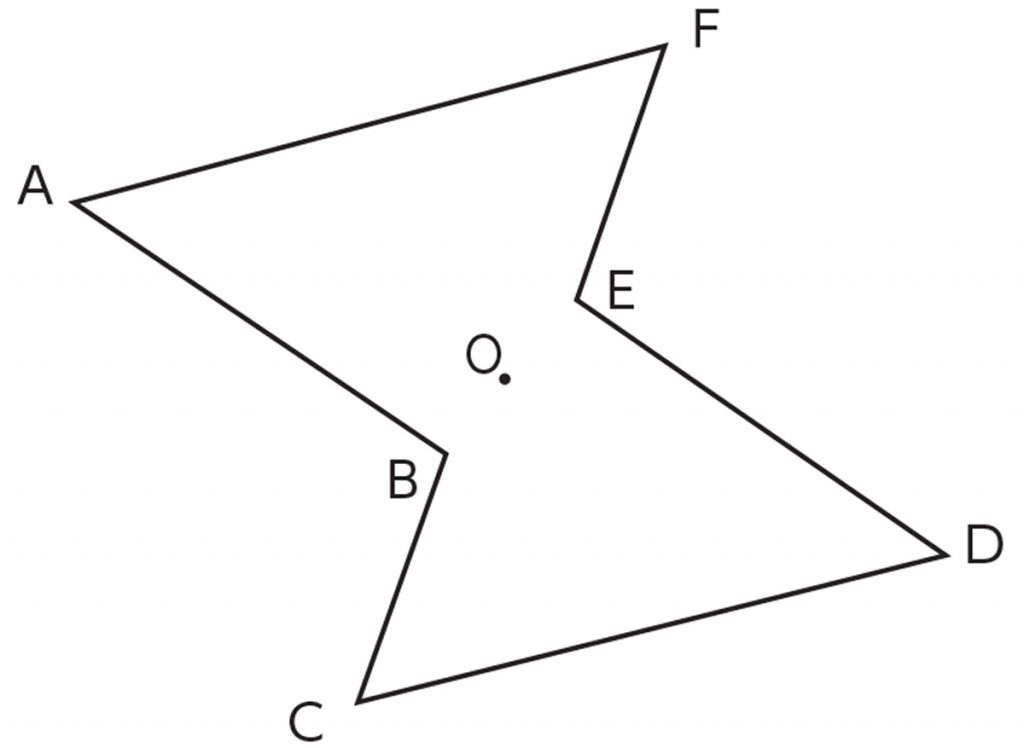



小6算数 点対称な図形の性質 指導アイデア みんなの教育技術
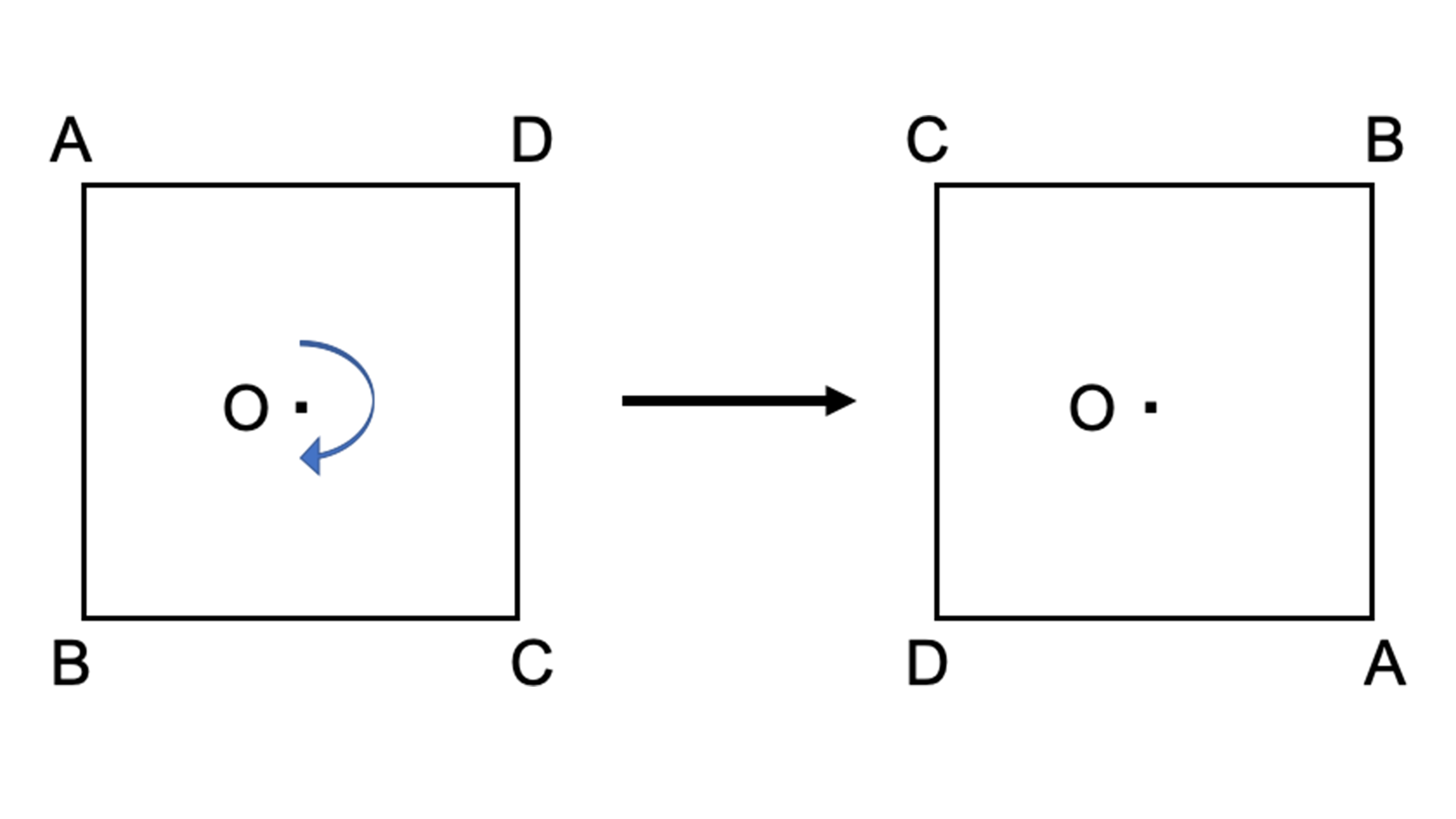



線対称との違いは 点対称 な図形を理解しよう お役立ち情報ページ 個別指導の学習塾なら個別指導塾スタンダード
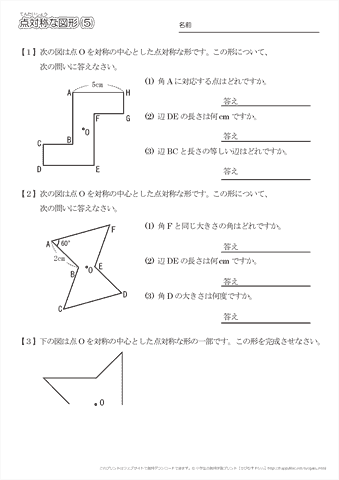



小学6年生の算数 点対称な図形 問題プリント ちびむすドリル 小学生




算数 対称な図形 問題の工夫
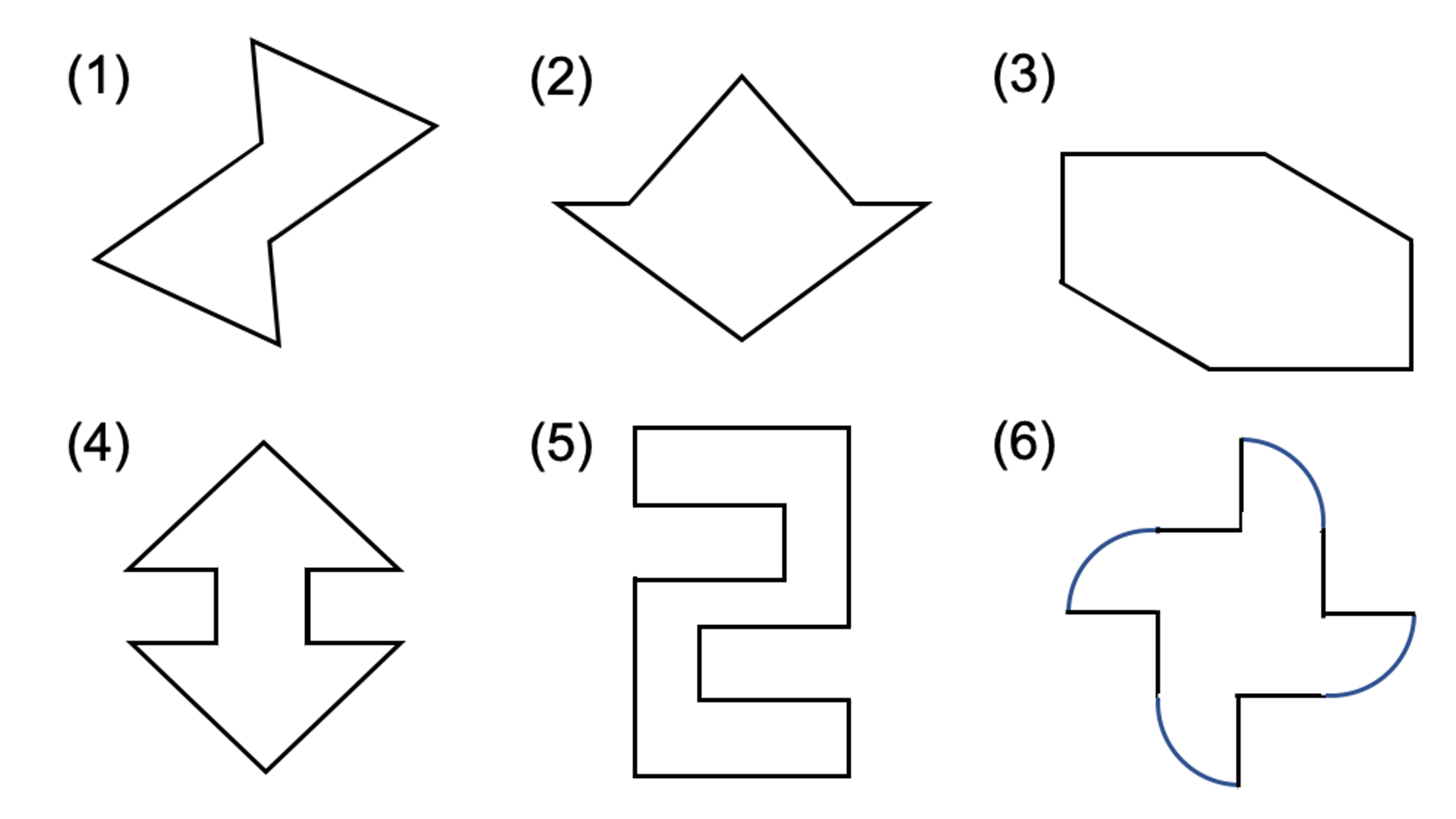



線対称との違いは 点対称 な図形を理解しよう お役立ち情報ページ 個別指導の学習塾なら個別指導塾スタンダード




小学6年生 算数 8月 線対称 点対称 円の面積 練習問題プリント 栄光ゼミナール ちびむすドリル 小学生学習教材 スペシャルコラボ
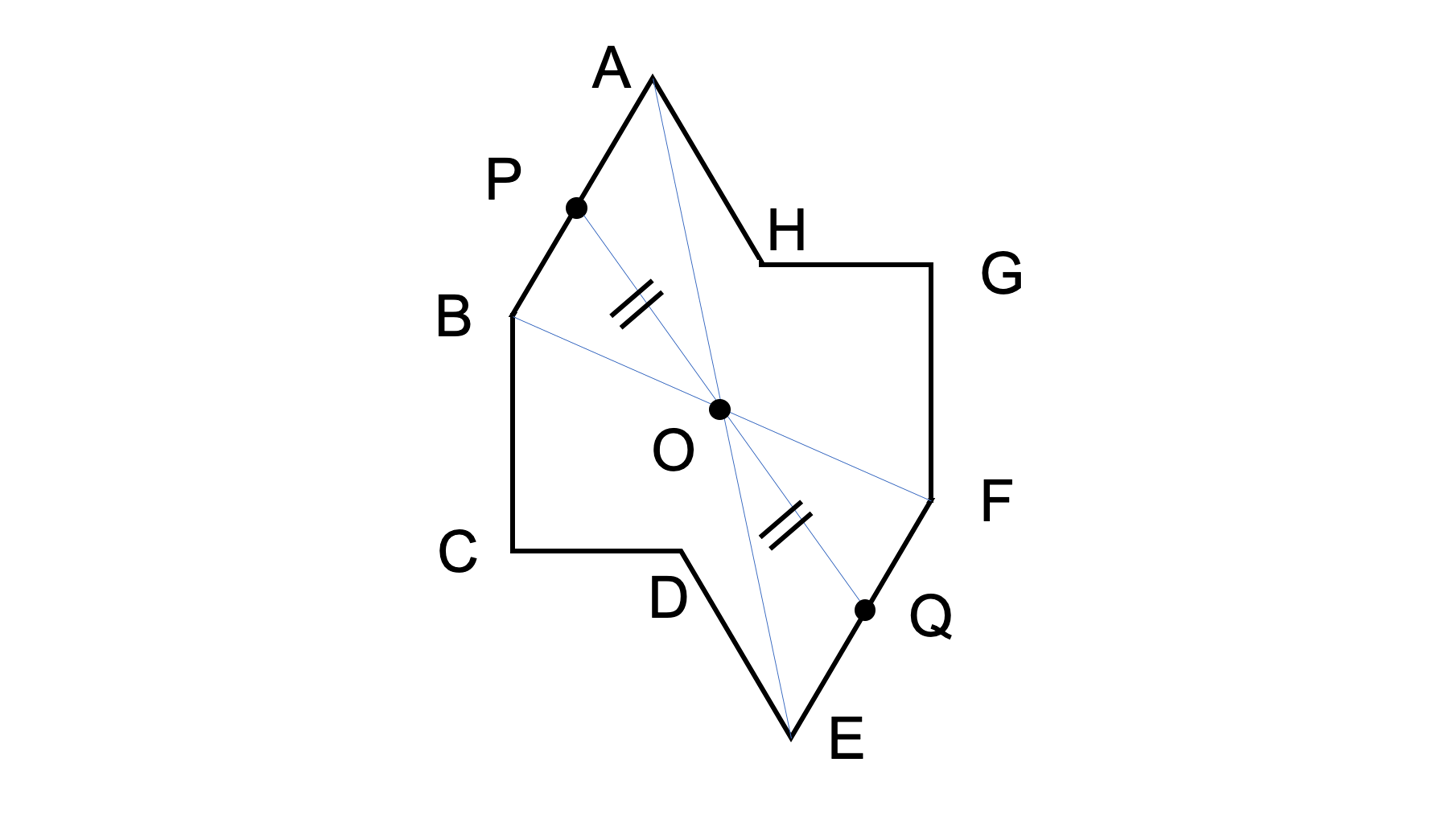



線対称との違いは 点対称 な図形を理解しよう お役立ち情報ページ 個別指導の学習塾なら個別指導塾スタンダード
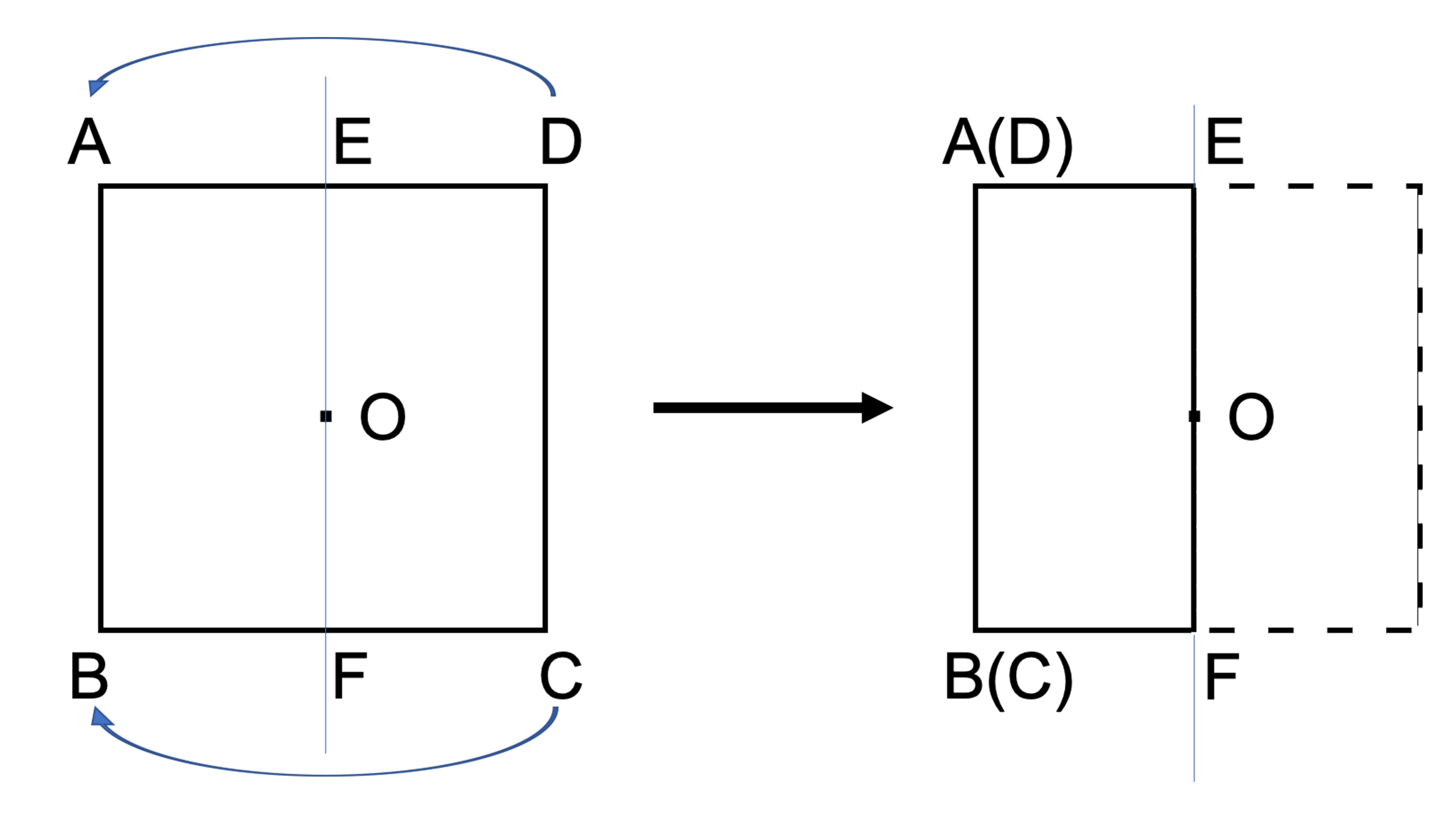



線対称との違いは 点対称 な図形を理解しよう お役立ち情報ページ 個別指導の学習塾なら個別指導塾スタンダード



Studydoctor線対称 点対称な図形の書き方 中学1年数学 Studydoctor
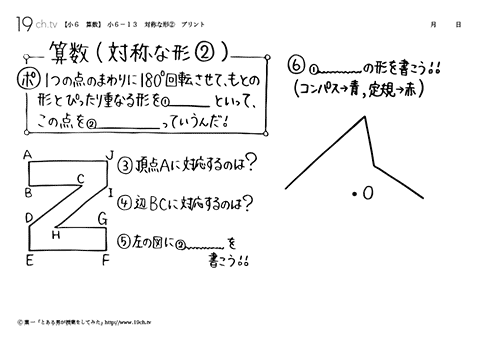



小学6年生の算数 動画 対称な形 の問題 19ch 点対称



1
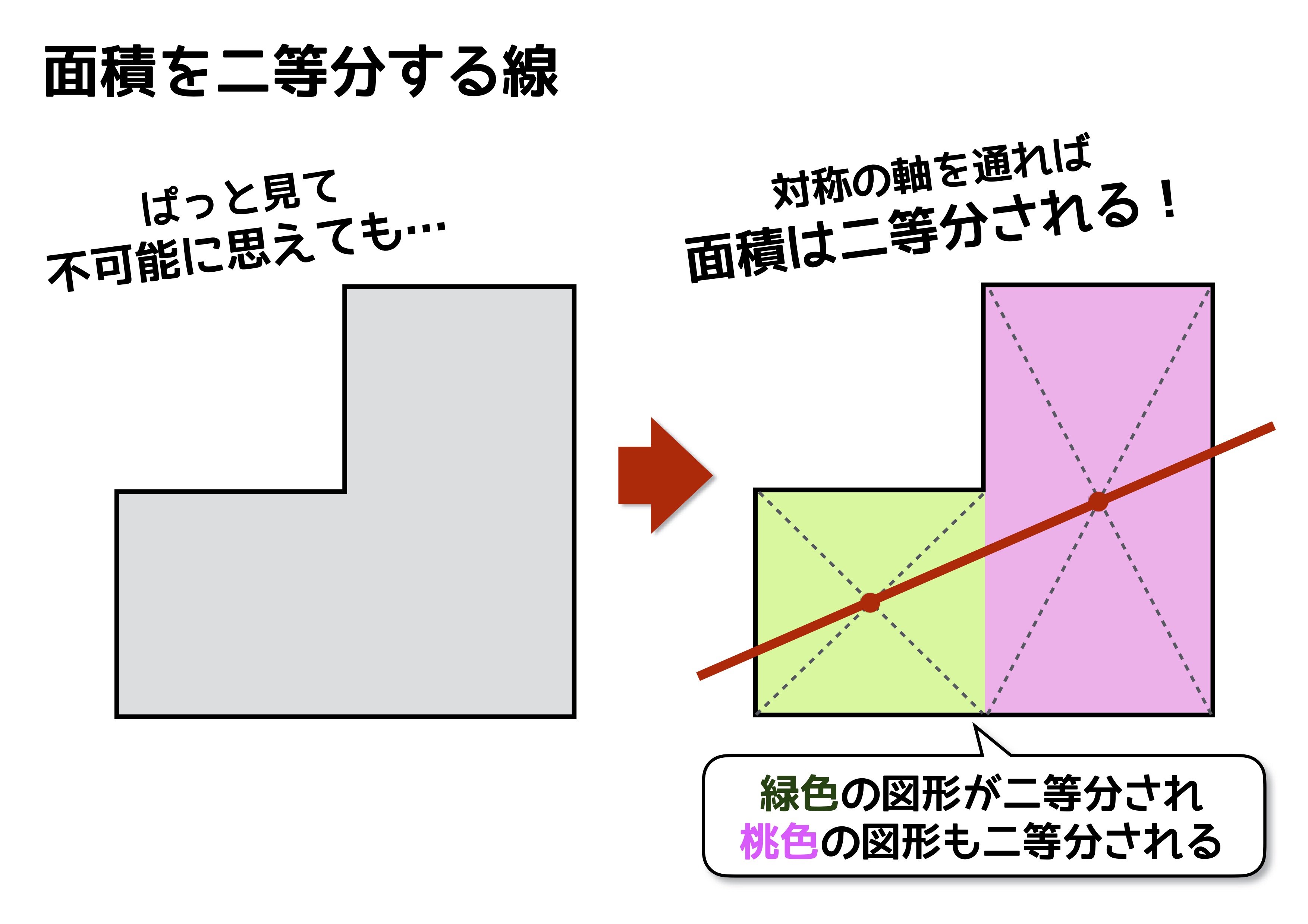



線対称と点対称 3つの性質を上手に使えるかどうかで得点に大きな差が出る 中学受験ナビ



Fdk3a7ctb5192box5b Com Es 6nen Mt Tentaishou Sakuzu Html



0 件のコメント:
コメントを投稿