が成り立つという有名な定理です ここでは, 三平方の定理 (平面上の定理)を3次元に拡張した, 四平方の定理を紹介します 定理 3つの面が直角三角形で, 1つの頂点に直角が集まっている三角錐を考えるとき, 直角三角形の面の面積を S1,S2,S3 S 1, S 2, S 3, 残りの三平方の定理の証明 三平方の定理はなぜ成立するのか。 ありとあらゆる直角三角形に成り立つというのです。不思議な気がしませんか? 実に様々な証明がありますが、 中学生が学習しておくべき最も重要な証明を紹介します。 三平方の 三平方の定理(ピタゴラスの定理): \angle C=90^ {\circ} ∠C = 90∘ であるような直角三角形において, a^2b^2=c^2 a2 b2 = c2 英語ですが,三平方の定理の証明を105個解説しているすさまじいサイトがあります。

tan8とcos8であらわした三平方の定理の覚え方 Schoolmath S Diary
三平方の定理 公式 一覧
三平方の定理 公式 一覧-三平方の定理の逆を証明する 三平方の定理の逆って、なんで成り立つの? 証明はどうすんの? ってことをお話していきます。 3辺の長さが の三角形において が成り立つならば、 ABCはcを斜辺とする直角三角形となることを証明せよ。 まずは、 が図形・三平方の定理 中学数学三平方の定理 導入 中学数学三平方の定理・例題 中学数学三平方の定理の証明 中学数学三平方の定理・特別な直角三角形 中学数学三平方の定理・円と接線、弦 中学数学座標平面上の2点間の距離




三平方の定理の証明と使い方
三平方の定理(ピタゴラスの定理)の公式をなんとなく覚えていた方も、なぜa 2 +b 2 =c 2 になるのか謎が解けたのではないでしょうか。 数学の公式は、原理・原則・定義に基づいて成り立っています。 三平方の定理とは 三平方の定理とは,直角三角形において各辺の関係は 斜辺 2 = 底辺 2 + 高さ 2 となる定理のことで、この定理のおかげで、 2辺の長さが分かればあと1辺の長さを求めることができる。三平方の定理とは、直角三角形の直角をはさむ2辺の長さを a, b, 斜辺の長さを cとしたときに、公式 a 2 b 2 = c 2 が成り立つという定理です。 ここで、斜辺とは、直角三角形の直角に対する対辺のことです。 三平方の定理は、別名、ピタゴラスの定理とも呼ばれます。
中3で学習する「三平方の定理」の中でも、これは応用問題です。例えば、こんな問題です。問題 上の図で、AB=、BC=21、CA=13です。 ABCの面積を求めなさい。まずは、三平方の定理までしか学習していない中3として、この問題をどう解くか考えてみま,セギ英数教室 角木優子 乗法公式を使ったルートの計算です。 今までは問題の中に高さが指定されていましたが、三平方の定理を学習すると、それを使ってまず高さを出さなければなりません。 少し大変ですが、重要事項なのでぜひ定着させてくださいね。三平方の定理は、別名『ピタゴラスの定理』と呼ばれます。 ピタゴラスは確か大昔の数学者です。 世界的にもこの定理は有名ですので少し解説していきたいと思います。 算数では様々な公式を覚えます。 しかしその公式の意味を知っている方は多く
三平方の定理とは、 「不思議な直角三角形」の不思議さを説明したもの です。 直角三角形は、上の図のような形をしていて、内側の 3 つの角のうち、 1 つが 90 度になっています。 三平方の定理(基礎) 直角三角形で2辺の長さがわかれば三平方の定理でもう1辺の長さが出ます。 定理に当てはめて計算するだけですが、ルートの計算を慎重に行ってくださいね。 今回は基本ですが、しっかり練習して慣れましょう。一方、3、4、5のような三平方の関係を満足する整数の組をピタゴラス数という。mとnを正の整数とすると(m>n)、 m 2 -n 2, 2mn, m 2 +n 2 はピタゴラス数になる。三平方の定理は平面や空間の2点間の距離の公式の基礎でもある。 柴田敏男



1




三平方の定理を簡単に理解 更に理解を深めよう 中学生 数学 公式 家庭教師のアルファ プロ講師による高品質指導
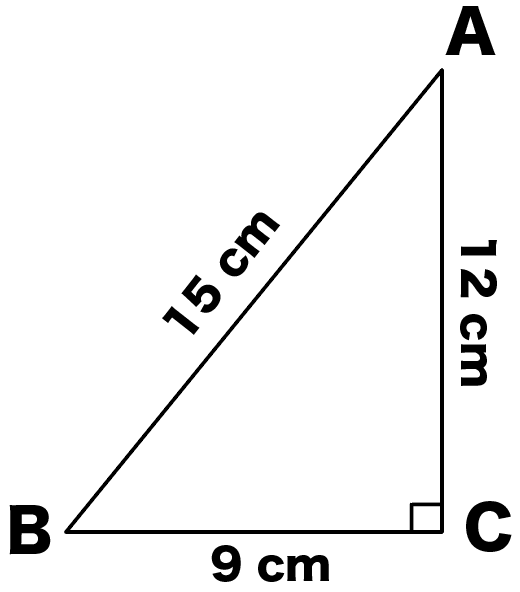
初等幾何学におけるピタゴラスの定理(ピタゴラスのていり、英 Pythagorean theorem )は、直角三角形の3辺の長さの関係を表す。 斜辺の長さを c, 他の2辺の長さを a, b とすると、定理は = が成り立つという等式の形で述べられる 。 三平方の定理(さんへいほうのていり)、勾股弦の定理(こう 辺の長さが2桁でも気にすんな。 三平方の定理(ピタゴラスの定理)の公式にぶち込めばいいんだ。 x² = 5² 12² x = 13 直角三角形と言えども、いつも右下に直角が来るとは限らんぞ。三平方の定理の証明|直感的に分かる図で解説します 管理人 5月 23, / 5月 27, 三平方の定理は直角三角形の辺の長さに関する定理ですが、今後、図形だけではなく関数などあらゆる分野でも利用することになる重要な定理です。 今回は三平方の定理




勉強しよう数学 拡張三平方の定理




三平方の定理 ピタゴラスの定理 の計算問題 の3つの解き方 Qikeru 学びを楽しくわかりやすく
1 三平方の定理 三平方の定理の歴史や由来を知る §1.ピタゴラス以前のピタゴラスの定理(古代エジプトとは紀元前3000年~紀元前30年) 古代エジプトではナイル川の氾濫で土地の区画が 分からなくなることがたびたびあったそうです。三平方_三辺の長さから三角形の面積を求める 三辺の長さがわかっている三角形の面積の出し方。 三平方の定理を利用して 方程式 をつくり、高さを求める。 ABCの面積を求めよ。 9cm 10cm 11cm A B C If playback doesn't begin shortly, try restarting your device Videos you watchヘロンの公式の証明(三角関数を使わずに) ヘロンの公式 は任意の 三角形 の3辺 a , b , c の長さから 面積S を求める公式である。 アレクサンドリアのヘロンが彼の著書『Metrica』の中で証明を与えていることから彼に帰せられる。 ただし, この証明には



3分でわかる 三平方の定理 ピタゴラスの定理 の公式とは Qikeru 学びを楽しくわかりやすく



1
三平方の定理(ピタゴラスの定理) ∠ACB=90°となる直角三角形ABCにおいて,各辺の長さを, BC = a , CA = b , AB = c とすると, a 2 b 2 = c 2 の関係が成り立つ.この関係を 三平方の定理 あるいは ピタゴラスの定理 という. 証明 三角比7|余弦定理は「三平方の定理」の進化版! があり, 正弦定理は 前回の記事 で説明しました. 余弦定理は直角三角形で成り立つ 三平方の定理の拡張で,これがどういうことか分かれば,そう苦労なく余弦定理の公式を覚えることができ ピタゴラスの定理とは、古代ギリシアの数学者で哲学者のピタゴラスが立ち上げた団体が発見した数学の定理のこと。 直角三角形をなす3辺のうち、2辺の長さを知ることができれば、残り1辺の長さを知ることができるというものです。 公式:a² b² = c²



図形 角度 面積問題 三平方の定理 中学生 練習問題45 60 75 3 4 5 の三角形 みんなの算数クラブ




三平方の定理 覚えておきたい基本公式を解説 数スタ
■次のような直角三角形の三辺の長さについては, a 2b 2=c 2 が成り立ちます.(これを三平方の定理といいます.) ■逆に,三辺の長さについて, a 2b 2=c 2 が成り立つとき,その三角形は直角三 三平方の定理とは、直角三角形において3辺の長さの関係を表す公式のことをいいます。 直角と隣り合う2辺の長さをそれぞれ a 、 b 、直角の向かい側にある最も長い辺 (斜辺)の長さが c となる直角三角形があるとします。三平方の定理とは? 三平方の定理とは、古代ギリシアの数学者である「ピタゴラス」の名前を取って、「ピタゴラスの定理」と呼ぶこともある定理で、「直角三角形の3辺の長さの関係」表す定理です。 直角三角形とは、中学数学で散々見てきた これですね。




知っていて当たり前 三平方の定理の応用 名寄 算数数学教室より



受験 定期試験 数学解き方集 裏技 解法 三平方の定理のテクニック 中学数学 高校数学
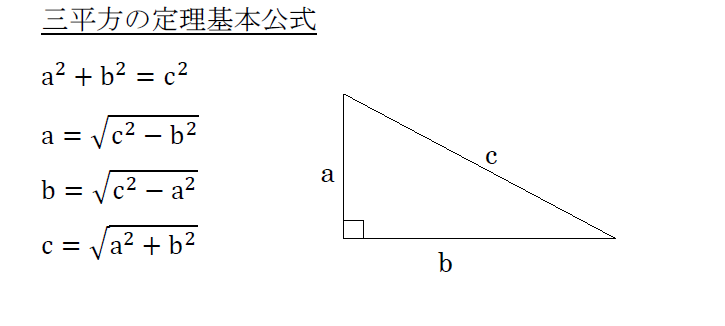
三平方の定理 基本の三平方の定理です。 直角三角形 の斜辺の二乗は底辺の二乗と高さの二乗になります。この公式は測量士補試験で頻繁に使うので必ず覚えてください。底辺(高さ)の長さを「1」として、三平方の定理に代入すると「斜辺 2 =底辺 2 高さ 2 ⇒ 斜辺 2 =11=2 ⇒ 斜辺=√2」になります。 よって、直角二等辺三角形の辺の比は「1:1;√2」です。 相似*円周角*三平方の定理などの高校で習う公式 (中3が使いやすいように改良笑)や自己流に編み出した公式集 ( ´ ` )ノ 自分用に作ったので見やすさは重視してません (=゚ω゚)ノ 数学 暗記 裏技 公式 円周角 三平方の定理 面積求め方 円錐 相似な図形




三平方の定理の練習問題10問 解き方の解説 数学fun
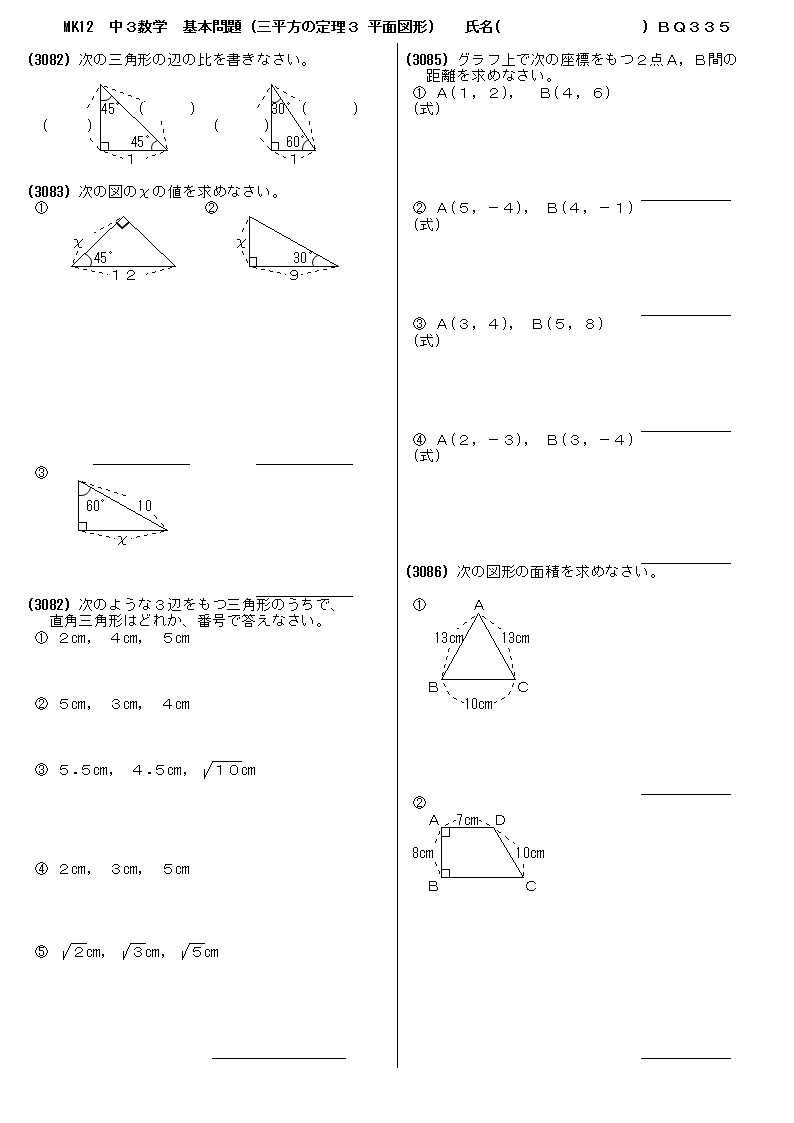



無料 中3数学 基本問題 問題プリント 335 三平方の定理3 平面図形




3分でわかる 三平方の定理の公式と証明 利用と問題例 合格サプリ




三平方の定理 無料で使える中学学習プリント




中3数学 三平方の定理とは 練習編 映像授業のtry It トライイット



三平方の定理




無料 中3数学 発展 応用問題 解答プリント 336 三平方の定理4 空間図形




3分でわかる 三平方の定理 ピタゴラスの定理 の公式とは Qikeru 学びを楽しくわかりやすく
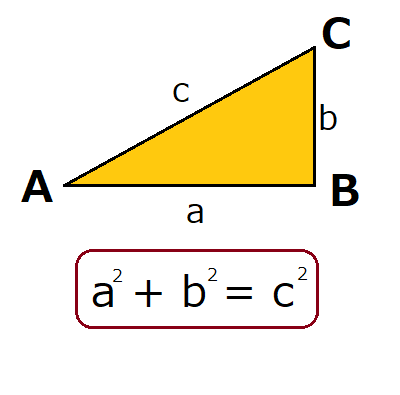



三平方の定理の証明 中学生向けの方法を6つ紹介 ヒデオの情報管理部屋




三平方の定理 覚えること 三角定規 苦手な数学を簡単に
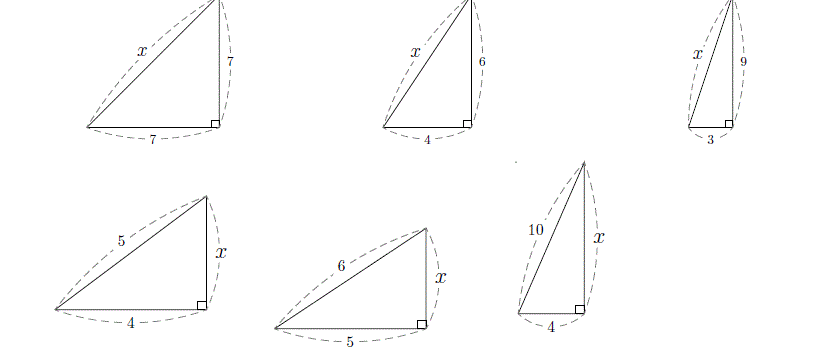



かみのドリル 三平方の定理




三平方の定理を慶應生が超わかりやすく解説 公式 証明 計算問題付き 高校生向け受験応援メディア 受験のミカタ




高校数学 三平方の定理による三角関数の計算 1 映像授業のtry It トライイット




数学 三平方の定理が成り立つ三辺の比 最重要7パターン 受験の秒殺テク 5 勉強の悩み 疑問を解消 小中高生のための勉強サポートサイト Shuei勉強labo




三平方の定理 直角三角形の辺の長さを計算する4つの問題の解き方 Qikeru 学びを楽しくわかりやすく




三平方の定理の証明と使い方




三平方の定理の逆はなぜ成り立つ わかりやすく解説 遊ぶ数学




中3数学 三平方の定理 で最も重要なポイントとは 映像授業のtry It トライイット



三平方の定理



Studydoctor三平方の定理の計算 中学3年数学 Studydoctor




感銘を受けた数学 三平方の定理の美しき証明たち 数学 統計教室の和から株式会社



中学数学の最後にして最大の壁 三平方の定理はこれで満点ゲット 高校入試徹底対策ガイド




三平方の定理を慶應生が超わかりやすく解説 公式 証明 計算問題付き 高校生向け受験応援メディア 受験のミカタ




勉強しよう数学 拡張三平方の定理




中3数学 三平方の定理とは 例題編 映像授業のtry It トライイット




感銘を受けた数学 三平方の定理の美しき証明たち 数学 統計教室の和から株式会社




三平方の定理を使って面積を求める方法は 問題を使って解説するよ 中学数学 理科の学習まとめサイト




3分でわかる 三平方の定理の公式と証明 利用と問題例 合格サプリ




中学3年生 数学 三平方の定理 練習問題プリント ちびむすドリル 中学生
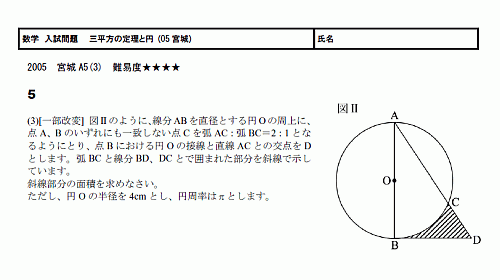



三平方の定理と円 スタディーx




世界が変わる裏技 三平方の定理を5秒で計算するテクニック Youtube
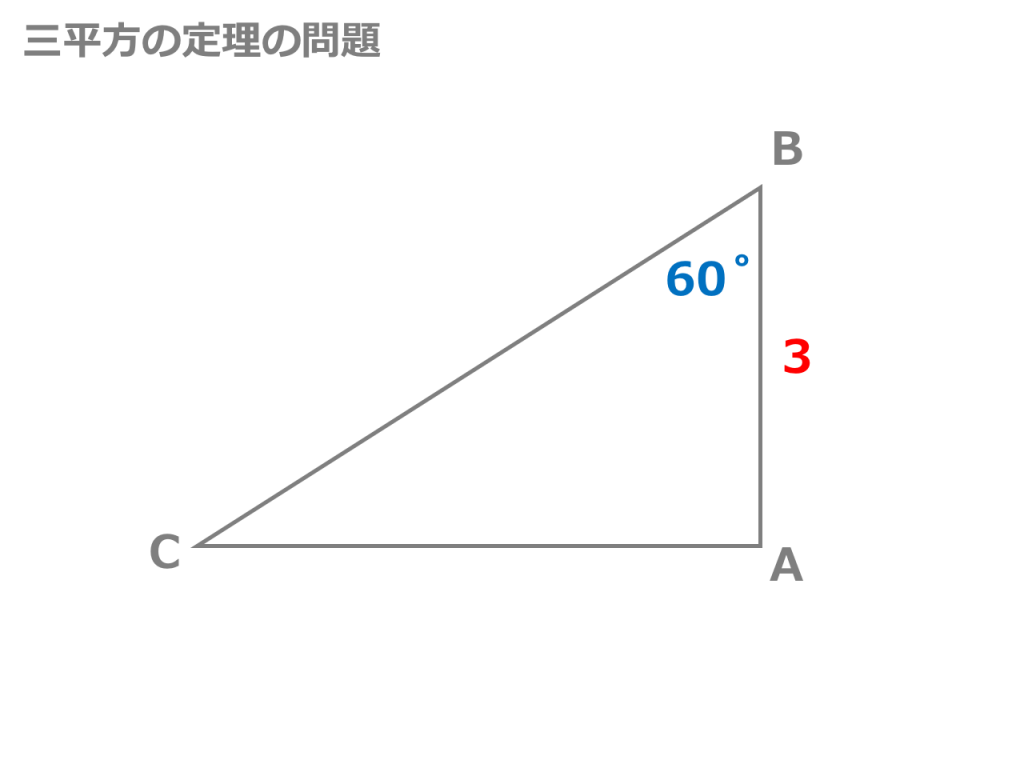



3分でわかる 三平方の定理の公式と証明 利用と問題例 合格サプリ
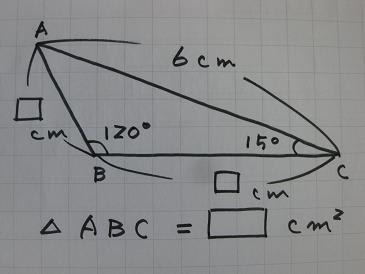



マッキーの教室 中2生徒の 三平方の定理 問題の質問に答える マッキーのつれづれ日記




三平方の定理について考える4 三角形の相似を使った証明方法 身勝手な主張




三平方の定理を慶應生が超わかりやすく解説 公式 証明 計算問題付き 高校生向け受験応援メディア 受験のミカタ




数学 中3 61 三平方の定理 基本編 Youtube




中3数学 図でよくわかる三平方の定理 ピタゴラスの定理 の証明と計算問題 Irohabook



1




三平方の定理を慶應生が超わかりやすく解説 公式 証明 計算問題付き 高校生向け受験応援メディア 受験のミカタ




三平方の定理の証明と使い方




ピタゴラスの定理と三角関数 たまには大学受験 灘校の教室 家庭教師 C O D Club
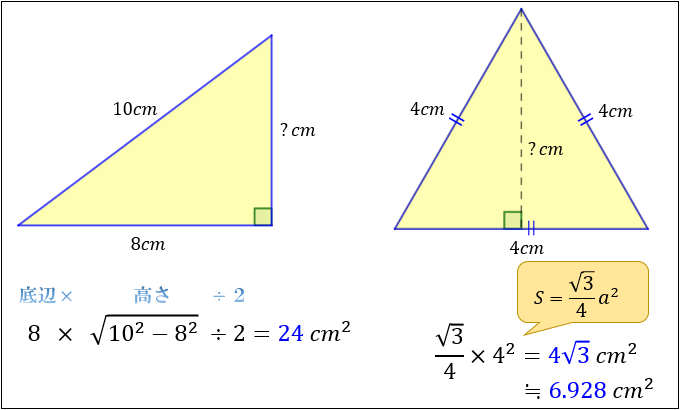



三角形の面積の求め方まとめ タイプ別でわかる公式一覧 アタリマエ




三平方の定理の計算 この問題は絶対にできるようになろう 中学や高校の数学の計算問題
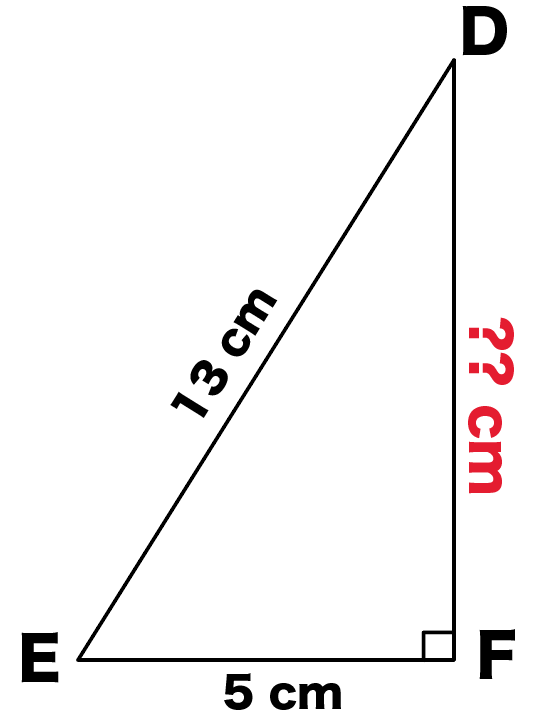



3分でわかる 三平方の定理 ピタゴラスの定理 の公式とは Qikeru 学びを楽しくわかりやすく




tan8とcos8であらわした三平方の定理の覚え方 Schoolmath S Diary




円を利用した三平方の定理の証明 数学の面白いこと 役に立つことをまとめたサイト




高校入試問題 全2問 標準レベルの三平方の定理を使う図形問題 Youtube




Excel 三平方の定理で直角三角形の辺の長さ 面積 角度を求める わえなび ワード エクセル問題集




必見 絶対知りたい三平方の定理の証明方法3選 見やすい図で即わかる 高校生向け受験応援メディア 受験のミカタ




中学3年生 数学 三平方の定理 練習問題プリント ちびむすドリル 中学生




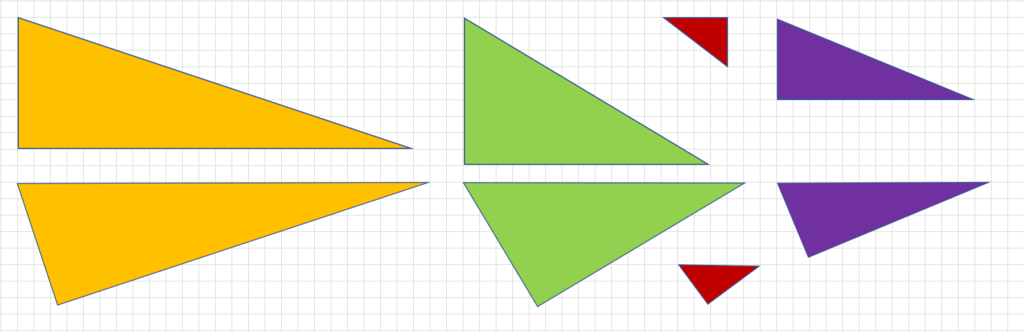
三平方の定理をパズルで証明 色んなパズルに挑戦してみよう 数学の面白いこと 役に立つことをまとめたサイト




中3数学 三平方の定理 で最も重要なポイントとは 映像授業のtry It トライイット




三平方の定理 特別な直角三角形の3辺の比 中学生からの勉強質問 数学 進研ゼミ中学講座
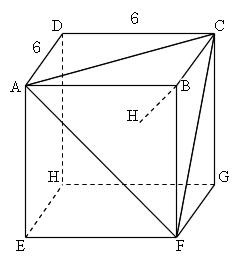



Mathematics 三平方の定理 5 空間図形と三平方の定理 働きアリ



三平方の定理が一瞬で理解できる 公式 証明から計算問題まで解説 Studyplus スタディプラス




三平方の定理を慶應生が超わかりやすく解説 公式 証明 計算問題付き 高校生向け受験応援メディア 受験のミカタ




三平方の定理の4通りの美しい証明 高校数学の美しい物語
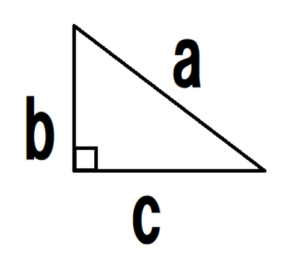



三平方の定理 公式を簡単に覚える方法 中学数学 札幌市 学習塾 受験 チーム個別指導塾 大成会




カーナビはなぜ正確なの その秘密 三平方の定理 で教えます 横山 明日希 ブルーバックス 講談社 1 4



名古屋市科学館 科学館を利用する 展示ガイド キーワード検索 ひ ではじまるキーワード キーワード ピタゴラスの定理 公式 と図形
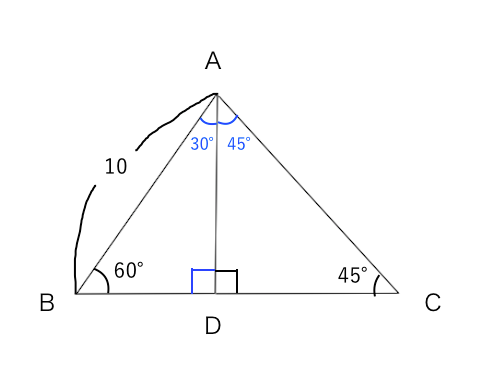



三平方の定理 練習問題 苦手な数学を簡単に




コラム ピタゴラスの定理 江戸の数学




Excel 三平方の定理で直角三角形の辺の長さ 面積 角度を求める わえなび ワード エクセル問題集




中3数学 三平方の定理の応用 75度に要注意 Youtube




三平方の定理と相似の問題 無料で使える中学学習プリント
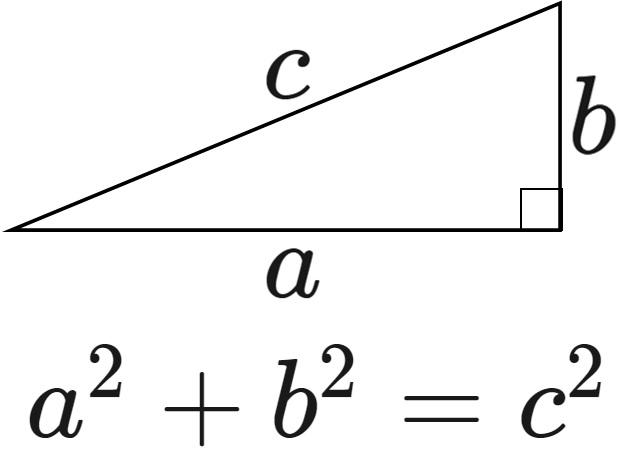



B Oc Hdjqqqofm



Studydoctor特別な三角形と三平方の定理 中学3年数学 Studydoctor



中3数学12 三平方の定理1 直角三角形 発展問題プリント 問題 333




三平方の定理の証明と使い方




三平方の定理 平面図形のいろいろな応用問題 無料で使える中学学習プリント




三平方の定理 ピタゴラスの定理 と公式の証明 忍者が用いた三角の知恵 アタリマエ




三平方の定理です 途中式含め教えてください Clear




中3数学 三平方の定理 で最も重要なポイントとは 映像授業のtry It トライイット




三平方の定理 ピタゴラスの定理 とは 応用問題パターンまとめ10選 遊ぶ数学




数学 三平方の定理が成り立つ三辺の比 最重要7パターン 受験の秒殺テク 5 勉強の悩み 疑問を解消 小中高生のための勉強サポートサイト Shuei勉強labo




無料 中3数学 発展 応用問題 解答プリント 334 三平方の定理2



三平方の定理とは 証明や計算問題 角度と辺の比の一覧 受験辞典




高校数学 第2余弦定理 三平方の定理の一般化 と第1余弦定理の証明と利用 受験の月



中学数学 直角三角形の三平方の定理とは ピタゴラス 平方根 の定理をexcelの図形で Curlpingの幸せblog




三平方の定理 特別な直角三角形の比を使った計算のやり方は Youtube




三平方の定理 ピタゴラスの定理 の計算問題 の3つの解き方 Qikeru 学びを楽しくわかりやすく




3分で理解 三平方の定理 ピタゴラスの定理 とその証明を完全解説 Rikeinvest



1
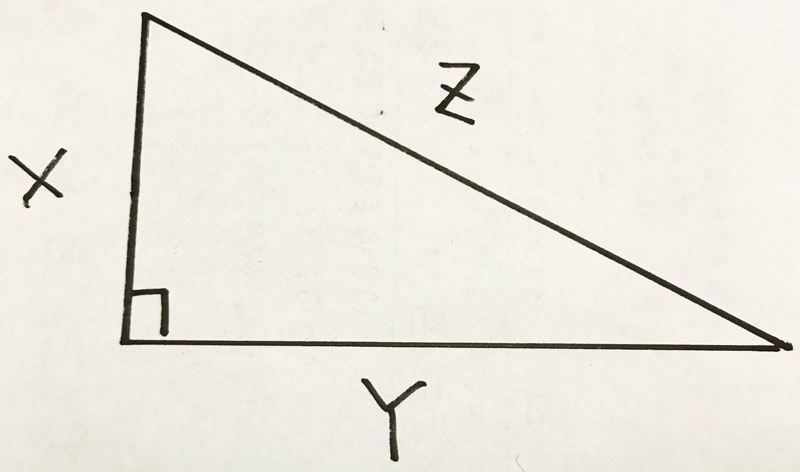



水平線までの距離 三平方の定理 21 3 19 茨木の法律相談 弁護士法人茨木太陽




三平方の定理を慶應生が超わかりやすく解説 公式 証明 計算問題付き 高校生向け受験応援メディア 受験のミカタ




中学3年生 数学 三平方の定理 練習問題プリント ちびむすドリル 中学生




三平方の定理 ピタゴラスの定理 の公式と計算方法 リョースケ大学




ピタゴラスの定理 Wikipedia




中学数学 三平方の定理 特別な直角三角形 中学数学の無料オンライン学習サイトchu Su




中3数学 三平方の定理 で最も重要なポイントとは 映像授業のtry It トライイット



中学数学の最後にして最大の壁 三平方の定理はこれで満点ゲット 高校入試徹底対策ガイド




三平方の定理 ピタゴラスの定理



三平方の定理が一瞬で理解できる 公式 証明から計算問題まで解説 Studyplus スタディプラス
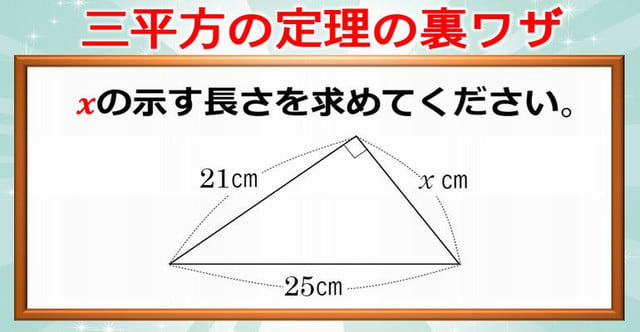



三平方の定理の裏ワザ 賢く解きたい計算の裏ワザ 暇つぶしに動画で脳トレ



0 件のコメント:
コメントを投稿